Sommario:- Ci sono prove secondo cui i poli avrebbero cambiato più volte posizione in passato. Questa possibilità, tuttavia, è sempre stata negata, poiché si ritiene che tale fenomeno sia fisicamente impossibile. L’articolo che segue dimostra la possibilità di spostamenti istantanei dei poli, dovuti all’impatto di corpi astronomici aventi un diametro dell’ordine del mezzo chilometro.

Introduzione

Charles Hapgood, nel suo libro “The Path of the Pole” (Chilton Book, Philadelphia, 1970), avanza l’ipotesi che durante il Pleistocene i poli si trovassero in posizione diversa da quella attuale e che addirittura abbiano cambiato posizione tre volte nel recente passato. Da una posizione nel mare della Groenlandia, raggiunta circa 70 mila anni fa, il polo nord si sarebbe portato in corrispondenza della Baia di Hudson all’incirca 50 mila anni, per spostarsi infine nella posizione attuale 11.600 anni fa, alla fine del Pleistocene.

A sostegno della sua ipotesi, Hapgood produce una impressionante quantità di prove, che in sintesi sono:

a) La presenza di calotte glaciali “polari” nel Nord America e nel Nord Europa, fortemente eccentriche rispetto al polo nord attuale.

b) La contemporanea assenza di ghiacci nella Siberia, la quale era anzi abitata, fin nelle sue regioni più settentrionali, da una imponente comunità ecologica.

c) Il mare Artico era più caldo di oggi, con presenza umana nelle isole della Nuova Siberia. 

d) L’Antartide era parzialmente libera dai ghiacci.

e) La situazione climatica generale della Terra era coerente con una posizione dei poli diversa da quella attuale

L’ipotesi che l’inclinazione dell’asse terrestre rispetto all’eclittica e che la posizione dei poli rispetto alla Terra possano variare è stata presa in considerazione fin dal secolo scorso. Alcuni fra i maggiori geologi dell’epoca, fra cui J.C. Maxwell e Sir George Darwin (figlio del più celebre Charles Darwin), si sono occupati del problema, arrivando alla conclusione che l’effetto stabilizzante dei rigonfiamenti equatoriali terrestri è talmente grande, che non c’è forza ipotizzabile in grado di provocare uno spostamento dell’asse di rotazione rispetto al pianeta stesso, a meno di una “collisione planetaria”. Essi pertanto hanno scartato l’idea di uno spostamento dei poli come impossibile ed in pratica non meritevole di discussione. La loro influenza è stata talmente decisiva, che nessuno, fino ad oggi, ha preso seriamente in considerazione tale ipotesi.

Lo stesso Hapgood accetta acriticamente il presupposto che soltanto una collisione planetaria  sarebbe in grado di provocare uno spostamento dell’asse di rotazione e propone pertanto, come meccanismo in grado di giustificare uno spostamento dei poli, quello dello “scorrimento” dell’intera crosta terrestre.

Basandosi sulle ricerche del geofisico russo V.V. Beloussov, egli ritiene che ad una profondità di circa 150 chilometri, nel mantello terrestre, esista uno strato di rocce allo stato liquido, che funzionerebbe come una sorta di “cuscinetto”, consentendo all’intera crosta terrestre di “slittare” rispetto al corpo della Terra, qualora sottoposta ad una forza tangenziale di grandezza adeguata. Tale forza sarebbe provveduta, secondo Hapgood, dal momento centrifugo di calotte glaciali eccentriche rispetto ai poli. In tal modo la Terra manterrebbe inalterato il suo asse di rotazione, ma i poli, e con essi l’intera superficie terrestre, “slitterebbero”, cambiando velocemente latitudine.

Prove che i poli, durante il Pleistocene, si trovassero in diversa posizione esistono in quantità impressionante, e questo spiega come  mai la teoria di Hapgood abbia attirato l’interesse di scienziati del calibro di Einstein e di K. F. Mather. Ma le difficoltà che essa solleva sono tante e tali da apparire altamente improbabile. Soprattutto essa è incompatibile con altre teorie geologiche che appaiono oggi irrinunciabili, come ad esempio la deriva continentale e la tettonica a zolle.

Inoltre la teoria di Hapgood non è in grado di spiegare alcune delle più significative peculiarità dei cambiamenti climatici pleistocenici, prima fra tutte la “rapidità” con cui sembrerebbe che tali cambiamenti si siano verificati. Secondo il meccanismo prospettato da Hapgood, infatti, il polo nord non può aver impiegato meno di due mila anni per portarsi dalla posizione di allora a quella attuale.  Le prove a disposizione, invece, porterebbero a concludere che i cambiamenti climatici siano stati estremamente più rapidi. Paradossalmente è proprio lo stesso Hapgood che mette in evidenza l’enorme complesso di prove che testimoniano la rapidità con cui gli spostamenti dei poli sarebbero avvenuti; rapidità che il meccanismo da lui proposto non è in grado di giustificare.

Sembrerebbe dunque che l’unico modo per spiegare completamente e coerentemente gli avvenimenti pleistocenici sia quello di ammettere la possibilità di spostamenti dei poli dell’entità ipotizzata da Hapgood, ma “istantanei”, che abbiano luogo cioè in un periodo di tempo dell’ordine dei giorni.

Questa possibilità è apertamente negata, come si è detto, ma a torto. Lo studio che segue, partendo da un’analisi del comportamento di un giroscopio perturbato, mostra come la coppia relativamente modesta sviluppata dall’impatto di un asteroide avente un diametro dell’ordine del mezzo chilometro, combinata con l’effetto di una coppia in apparenza trascurabile come quella esercitata dall’attrazione lunisolare sui rigonfiamenti terrestri, è in grado di provocare cambiamenti pressoché istantanei dell’asse di rotazione terrestre e quindi “salti” istantanei dei poli in qualunque direzione e per qualsiasi ampiezza.

Componenti rotazionali
di un giroscopio libero perturbato

Le componenti rotazionali in un giroscopio libero perturbato sono legate fra loro dalla seguente relazione, dovuta al Laplace, la quale esprime il principio della conservazione dell’energia:

1)            J_o W²  = J_o w²  + J_p w_p²  =  J_i w_i ²

dove:

W   =   velocità di rotazione del giroscopio non perturbato
         w = velocità di rotazione del giroscopio intorno al suo asse principale
         w_p = velocità di precessione
         w_i    =  velocità di rotazione istantanea del giroscopio
         J_o   =  momento d’inerzia principale del giroscopio
         J_p    =  momento d’inerzia rispetto all’asse di precessione
         J_i    =  momento d’inerzia rispetto all’asse di rotazione istantanea

Il valore della coppia perturbatrice sviluppata da una forza generica F_p, formante un angolo  b con l’asse di figura del giroscopio, è dato evidentemente dalla:

2)            C_p  =  R  F_p senb

dove R è il braccio della forza, ossia la distanza del suo punto di applicazione dal centro del giroscopio. 

 Il movimento di precessione w_p del giroscopio avviene sempre intorno ad un asse equatoriale, che però è diverso istante per istante in modo tale che l’asse di figura viene a muoversi su una superficie conica, con vertice al centro e apertura 2 b. Esso viene quindi a ruotare con velocità angolare w_pa intorno ad un asse parallelo alla forza stessa, che chiameremo asse di precessione apparente, per distinguerlo da w_p (vedi fig. 1).

Il valore della w_pa è dato dalla formula :

3)       

                          

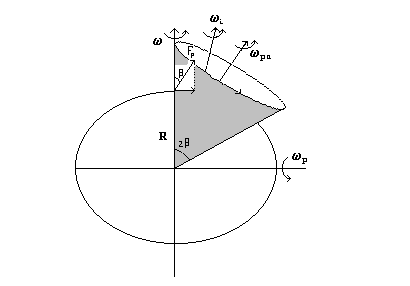
fig.1

Le relazioni 1), 2) e 3) consentono di studiare esaurientemente il comportamento di un giroscopio libero perturbato, con un metodo essenzialmente grafico. 

Dato un giroscopio, disegniamo, sulla base della sua ellisse di inerzia, un’altra ellisse i cui semiassi siano rispettivamente:

                      

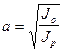
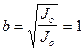
Ciascun raggio  dell’ellisse r(q) , con q  = 0  ¸  2p, avrà ovviamente il valore:        

dove J _q  è il momento d’inerzia di un asse formante un angolo q  con quello di figura.

Posto  W²  =  1 , per la 1) ciascun raggio r(q) è proporzionale alla velocità angolare che il giroscopio deve avere intorno all’asse q  per mantenere invariata l’energia iniziale (vedi fig.2)

Le estremità delle frecce rappresentanti W ed w_i , quindi, cadono sempre sull’ellisse, mentre tutte le altre componenti rotazionali si trovano sempre all’interno di essa. Questa ellisse consente di analizzare esaurientemente il comportamento delle varie componenti rotazionali del giroscopio, legate come sono dalla relazione 1).

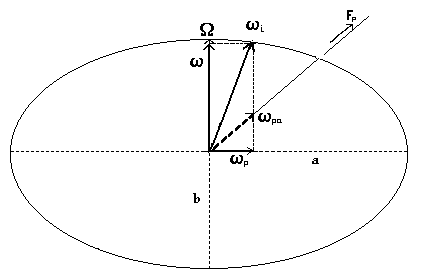
fig. 2

Il significato di queste componenti è facilmente intuibile. Un giroscopio soggetto ad una coppia di ribaltamento reagisce sviluppando una coppia esattamente uguale e contraria. Questo viene ottenuto ruotando istante per istante intorno ad un asse, w_i ,  diverso da quello di figura e tanto più sbilanciato quanto più grande è la coppia perturbatrice. La w_i è la risultante del movimento di rotazione attorno all’asse di figura  e della rotazione, w_p,  attorno ad un asse equatoriale. In ogni istante si ha ovviamente: w_i² = w² + w_p².

Quando un giroscopio è soggetto ad una coppia perturbatrice Cp, di valore crescente, w_p cresce, per cui la w_i si sposta in direzione della w_pa.

Quando la F_p raggiunge un valore F_pa uguale a quello sviluppato dal giroscopio ruotante intorno all’asse di w_pa  (vedi calcoli più avanti),avremo evidentemente ;

w_i = w_pa.

In questo momento l’asse di rotazione istantanea viene a coincidere con l’asse di precessione apparente. E’ questa una condizione particolarissima in cui il sistema costituito dal giroscopio e dalla coppia perturbatrice si comporta come un giroscopio non perturbato, con un’unica componente rotazionale, W’, fissa rispetto allo spazio ed al corpo giroscopico stesso, il cui asse diventa asse di rotazione principale del sistema.

Se a questo punto la forza F_p torna a diminuire, il sistema di comporta come un giroscopio cui venga applicata una coppia di valore:

C’_p = C_pa  - C_p

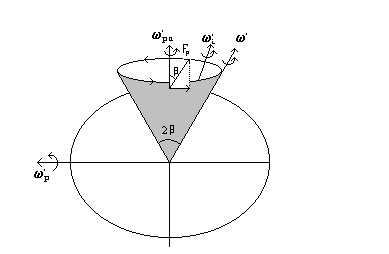
fig. 3

Il nuovo asse di rotazione comincia pertanto a precedere intorno all’asse di figura; la w_i’, di conseguenza ripercorre il cammino inverso, portandosi in direzione di quest’ultimo. Il valore e la direzione delle varie componenti rotazionali del giroscopio in questo caso sono rappresentati in fig.3 e 4.

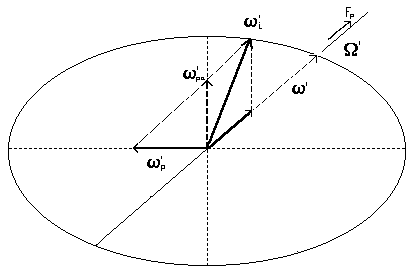
fig. 4

Per il principio di conservazione dell’energia, si avrà evidentemente:

J_pa W’² =  J_o w’² + J’_pw_p’²  =  J_i w_i’² = J_o W²

A parità di forza perturbatrice F_p,  la velocità di rotazione istantanea è esattamente la stessa sia nel tragitto di “andata” che in quello di “ritorno”. Si ha cioè sempre w_i’ =  w_i . Variano invece in maniera sostanziale le altre componenti rotazionali. In particolare w’_p ha direzione opposta a  w_p . Questo si giustifica con il fatto che mentre nel tragitto di “andata” è l’asse di figura che ruota intorno all’asse di  w_pa , in quello di “ritorno” avviene il contrario, e cioè l’asse di  w_pa, che ora è fisso rispetto al corpo del giroscopio, viene a ruotare intorno a quello di figura.

Essenziale è il fatto che lungo l’asse di  w_pa si ha una componente rotazionale fissa rispetto al corpo del giroscopio. Ciò significa che il giroscopio conserva “memoria” della posizione del nuovo asse di rotazione. La componente rotazionale, e con essa la “memoria”, vengono cancellate soltanto quando la F_p si annulla totalmente. Se la F_p non dovesse annullarsi, il giroscopio conserverebbe indefinitamente due componenti rotazionali, entrambi intorno ad assi fissi rispetto a se stesso.

Comportamento di un giroscopio semifluido come la Terra

Il comportamento della Terra in presenza di una coppia perturbatrice è assimilabile a quello di un giroscopio, con una importante differenza, dovuta al fatto che il pianeta non è un solido omogeneo e indeformabile, ma è costituito da parti interne ed esterne liquide e da un guscio solido intermedio, dotato di alta plasticità e facilmente deformabile sotto l’effetto delle forze centrifughe. Ogni componente rotazionale del pianeta esercita sulle sue parti una forza centrifuga, in conseguenza della quale si hanno deformazioni e/o movimenti di massa, che a loro volta influiscono sulle componenti rotazionali e tendono costantemente ad annullare ogni eventuale coppia di reazione.

Se ad esempio costringiamo un giroscopio indeformabile a ruotare intorno ad un asse diverso da quello di figura, esso sviluppa una coppia di reazione che rimane costante nel tempo.

Anche la Terra, costretta a ruotare intorno ad un asse diverso da quello di figura, svilupperebbe inizialmente una coppia di reazione. La stessa forza centrifuga responsabile di questa coppia, tuttavia, agirebbe sulle masse plastiche e liquide, provocando deformazioni e/o spostamenti, tendenti a ricostituire l’ellissoide intorno al nuovo asse di rotazione. Di conseguenza la coppia di reazione diminuirebbe, fino ad annullarsi completamente dopo un certo tempo.

Noi non conosciamo forze in grado di costringere la Terra a ruotare intorno ad un asse diverso da quello di figura per un tempo sufficientemente lungo a completare un tale processo. Sappiamo, però, che il pianeta viene periodicamente colpito da grandi bolidi ad alta velocità, i quali sviluppano una coppia di ribaltamento di durata molto breve, ma che può avere un valore di picco assai elevato, dello stesso ordine di grandezza della coppia di reazione massima sviluppabile dalla Terra (vedi al paragrafo successivo i relativi calcoli).

Vediamo, con l’ausilio dei grafici di fig.2 e 4 cosa succede in questo caso.

Non appena la coppia sviluppata dall’impatto comincia a crescere, la w_i si porta in direzione della w_pa , parallela alla direzione dell’urto, fino a coincidere con essa se l’impatto sviluppa una coppia impulsiva di intensità sufficiente. In quell’istante l’asse di w_pa diventa asse permanente. Non appena la coppia impulsiva  diminuisce, l’asse w_i torna velocemente in corrispondenza di quello di figura iniziale, ma con modalità radicalmente diverse da quelle del tragitto di “andata”, come si vede da fig. 4 Non appena l’impulso cessa, un attimo dopo, la Terra dovrebbe tornare nuovamente a ruotare intorno al suo asse naturale e tutto dovrebbe finire lì, ma non è detto.

Perché la “memoria” del nuovo asse di rotazione venga cancellata  ed il giroscopio torni a ruotare intorno all’asse di figura, è necessario che la coppia perturbatrice si annulli “completamente”. Purtroppo, ci sono buone probabilità che questo non avvenga. Sappiamo che la Terra è soggetta in permanenza ad una coppia perturbatrice dovuta all’attrazione gravitazionale esercitata dal sole e dalla luna sui rigonfiamenti equatoriali. Questa coppia è di un ordine di grandezza dieci milioni di volte più piccolo di quella sviluppata dall’urto; ma il suo ruolo è fondamentale.

  Se al momento dell’impatto essa ha segno contrario rispetto a quello sviluppato nell’urto, appena l’impulso si esaurisce, la Terra recupera istantaneamente il primitivo asse di rotazione e tutto finisce lì. Gli unici effetti sarebbero quelli distruttivi immediati prodotti dall’impatto.

Se invece essa ha inizialmente la stessa direzione della coppia impulsiva prodotta dal bolide, si somma a quest’ultima e contribuisce, nel suo piccolo, allo spostamento subitaneo della posizione dei poli.  Pochi istanti dopo, la coppia impulsiva si annulla, ma quella lunisolare rimane e, per quanto piccola, è pur sempre maggiore di zero e quindi sufficiente ad impedire che la “memoria” dell’asse intorno a cui la Terra ha ruotato per un breve istante venga cancellata.

In questo caso la Terra viene a comportarsi in realtà come un giroscopio con asse di figura coincidente con quello assunto nell’istante  dell’impatto, soggetto ad una coppia perturbatrice costante, di entità praticamente uguale e segno contrario a quella impulsiva sviluppata dal bolide. Vediamo in figura 5 la situazione che si viene a determinare in questo caso.

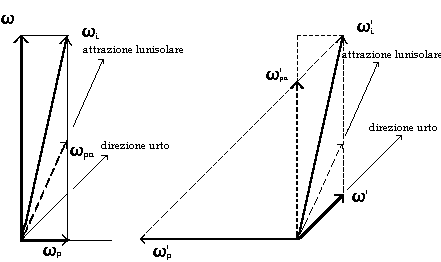                    a                                                           b

   fig. 5

I grafici 5.a e 5.b rappresentano la situazione delle componenti rotazionali della Terra immediatamente prima (a) e dopo (b) l’impatto, nel caso in cui la coppia lunisolare abbia lo stesso segno di quella sviluppata dall’urto. (Nella figura le componenti rotazionali di precessione sono molto esagerate, ai fini esplicativi; in realtà sono dell’ordine del milione di volte più piccole della rotazione principale. Il ragionamento, tuttavia, non cambia).

La situazione in apparenza non è cambiata, perché w_i  è esattamente uguale ad w’_i, ed anche w’ è dello stesso ordine di grandezza della velocità di precessione iniziale w_pa, milioni di volte più piccola della rotazione principale .

C’è però una differenza fondamentale: a questo punto la  w’ è l’unica componente rotazionale “fissa” rispetto al corpo della Terra. L’asse di  w’ , quindi, è asse di rotazione permanente e per quanto piccola sia la rotazione intorno ad esso (un milione di volte più piccola della rotazione principale), esso esercita pur sempre una forza centrifuga, debolissima, che tende a formare un rigonfiamento equatoriale rispetto al proprio asse (che sarebbe dell’ordine della decina di metri).

Se la Terra fosse un giroscopio rigido indeformabile, questa situazione permarrebbe immutata indefinitamente. Il pianeta, però, è coperto da un sottile strato di acqua, molto pronta a reagire ad ogni cambiamento di moto.

Si comincia quindi con l’avere un leggero spostamento di liquidi verso la nuova linea equatoriale. Mano a mano che ciò avviene, la  w’ torna ad aumentare, quindi cresce la forza  tendente a far spostare i liquidi verso il nuovo equatore, e così via, in un processo che parte molto lentamente, ma va via via accelerandosi fino a che la forza centrifuga non diviene sufficiente far deformare il guscio plastico. Dopo un certo tempo, quindi, l’ellissoide si ricostituisce intorno al nuovo asse di rotazione, e la Terra torna nuovamente in condizioni di stabilità, ma con asse di rotazione e poli spostati.

Il meccanismo qui su illustrato dimostra che i poli terrestri, contrariamente a quanto si è sempre ritenuto, possono “saltare” pressoché istantaneamente da una posizione ad un’altra distante anche migliaia di chilometri, sotto l’effetto combinato di forze apparentemente insignificanti, quale l’urto di un asteroide e la forza di attrazione lunisolare sui rigonfiamenti equatoriali.

Resta da valutare ora quale sia la probabilità che ciò accada. Secondo Hapgood si sarebbero verificati tre salti di poli negli ultimi 100mila anni soltanto, il che significa che la probabilità di un avvenimento del genere sarebbe estremamente elevata. Per poterla valutare occorre innanzitutto determinare il valore della coppia di reazione sviluppata dalla Terra e di qui calcolare le caratteristiche dimensionali e cinematiche che un corpo celeste deve avere per uguagliarla.

Valore della coppia di reazione della Terra

Il valore della coppia di reazione di un giroscopio, quando ruota intorno ad un asse diverso da quello di figura, può ricavarsi (vedi fig. 6), considerando la coppia elementare sviluppata dall’elemento di massa dm, che gira intorno all’asse di rotazione istantanea w_i:

C_i  =  F_i b

                            

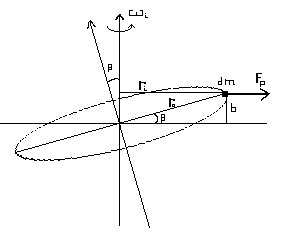
fig. 6

dove:     

   F_i  =  dm w_i²  r _i   = dm  w_i²  r_o cos b       è la forza centrifuga;

   b   =  r_o senb     è il braccio della coppia.

 

Avremo perciò:

C_i  =  dm  r_o²  w_i² senb cosb =  dJ_o w_i² senb cosb = ½ dJ_o w_i² sen2b

dove dJ_o = dm r_o²  è il momento d’inerzia della massa dm rispetto all’asse principale.

Per un giroscopio costituito da un ellissoide di rotazione avremo pertanto (vedi fig. 7):

 

4)  C =  (J_o - J_p) w_i² senbcosb  = ½   J_r w_i² sen2b

dove J_r = (J_o - J_p)  è il momento d’inerzia del solo rigonfiamento equatoriale.

 

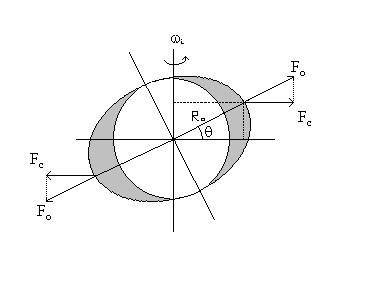
                fig7        

               

 

Dalla relazione 4) si vede che un giroscopio è in grado di sviluppare una coppia di reazione soltanto quando J_o ¹ J_p. Se fosse una sfera perfetta, infatti, esso ruoterebbe indifferentemente intorno ad un qualsiasi asse e non si avrebbe alcuna componente stabilizzante. In una sfera omogenea, infatti, tutte le forze centrifughe si bilanciano reciprocamente e non si ha alcuna coppia di reazione, qualunque sia l’asse di rotazione. Soltanto i ‘rigonfiamenti” sviluppano una coppia di reazione, quando ruotano intorno ad un asse diverso da quello di figura

 

 

Valore della coppia stabilizzante sviluppata dai rigonfiamenti terrestri

 

Dalla 4) si vede che la coppia di reazione massima sviluppabile da un giroscopio è:

  

C_m = ½ J_r  w_i²

 

Il valore di w_i  è sensibilmente uguale a quello della rotazione normale, per cui possiamo porre:

w_i²   »  (2p / 8,64)² 10¹⁰ =  5,28 . 10⁹

 

Il calcolo della J_r può essere fatto in modo indiretto, utilizzando i calcoli sviluppati da Gallen e da Deininger per conto dello stesso Hapgood (vedi riquadro a parte), la forza centrifuga sviluppata dai rigonfiamenti equatoriali per effetto della rotazione terrestre è pari a:

 

F_o   = 4,1192. 10¹⁹  kg.

Per un calcolo approssimativo possiamo porre:

J­_r @ M­_r R_o²

F_o @ M_r w_i² R_o² = J_r w_i² / R_o

dove M_r è la massa dei rigonfiamenti ed R_o il raggio della Terra.

              

Si ha quindi:

 

J_r =  F­_o R_o / w_i² @  5 10³⁴ kgmt² 

Ed infine, grazie all’equazione 4), avremo:

4’)           C = ½ J_r w_i²  sen2b = 1,38 sen2b   kgmt.

Per b = 45^o avremo:

C @ 1,38 10²⁶ kgmt

che è la massima coppia di reazione sviluppabile dalla Terra.

Calcolo della massa che un asteroide deve possedere per provocare un salto di poli

Per la relazione 4) un asteroide che colpisca la Terra, per spostare l’asse di rotazione di un certo angolo, ad esempio di 20° (per un solo istante si intende), deve poter sviluppare una coppia impulsiva di valore:

C_20°   =   8,87 . 10 ²⁵  Kgmt. 

E’ pertanto immediato calcolare le caratteristiche dimensionali e cinematiche che tale corpo deve possedere.

La forza  impulsiva F_i sviluppata nell’impatto con la Terra è data dalla formula classica:

F_i = M_a a

dove

a = dv/dt       è l’accelerazione che il corpo subisce nell’impatto

M_a                   è la  massa dell’asteroide

Per il calcolo dell’accelerazione, a, possiamo assumere che l’asteroide al momento dell’impatto abbia una velocità,  v, compresa fra 25 e 75 km/sec., cioè la media di quella constatata per gli oggetti Apollo. Poniamo pertanto:

v = 5 . 10 ⁴  mt/sec.

Per il calcolo di dt dobbiamo affidarci ad una stima. In via del tutto prudenziale, basandoci sulla profondità dei crateri conosciuti, possiamo assumere che la profondità del  cratere provocato dall’impatto sia di ½  km; ciò significa che la velocità del corpo passa da 5.10⁴ mt/sec a 0, nello spazio di ½  chilometro. Possiamo valutare l’intervallo di tempo in cui ciò avviene nell’ordine del centesimo di secondo, cioè:    

dt  = 0,01 sec.

L’accelerazione media subita dal corpo sarà pertanto:

a_m  =  dv/dt  =    5.10⁴ / 0,01  = 5. 10⁶  m/sec²

Il picco di accelerazione è certamente molto superiore; per un calcolo prudenziale possiamo assumere che sia il doppio del valore medio. Si avrà pertanto:

a = 5.10 ⁴  / 0.005  =   10 ⁷  mt/sec²

E pertanto si avrà:

F_i  =  M_a .  10 ⁷   kg

La coppia sviluppata da questa forza sarà evidentemente :

C_i  =  F_i . R_i

dove:      R_i  è il braccio della forza.

Il valore di R_i può essere compreso fra 0 e R_o@6,4 10⁶ mt., e cioè il valore del raggio terrestre. Per ragioni statistiche possiamo porre:

R_i = ½ R_o = 3,2 10⁶ mt

  

Il valore della massa dell’asteroide sarà pertanto:

 

    

 

Supposto che il corpo abbia una densità di 3 Kg/dm³, si ha un volume di:

V_a  =  0,92 km³

Un asteroide litico, quindi, del diametro dell’ordine del chilometro.  Questo calcolo, tuttavia, è prudenziale, per cui possiamo realisticamente ritenere che un oggetto avente un diametro dell’ordine del mezzo chilometro sia ampiamente sufficiente a sviluppare una coppia del valore richiesto per un salto di poli di grande ampiezza.

Probabilità che un impatto dia luogo ad un salto di poli

 

Perché l’impatto da parte di un corpo celeste dia luogo ad un salto dei poli, è necessario che siano verificate le due seguenti condizioni:

a)            che la coppia  d’impatto sia sufficiente a eguagliare la coppia di reazione massima della Terra nella direzione dell’urto, anche per un solo istante. Ciò significa che non solo il corpo deve avere massa e velocità adeguate, ma che anche il braccio della coppia deve essere sufficientemente ampio .

b)            La coppia di attrazione lunisolare sui rigonfiamenti terrestri deve avere lo stesso segno di quella sviluppata dall’impatto.

 

Questa seconda condizione ha chiaramente una probabilità di essere verificata del 50%. Quindi, in ogni caso la probabilità che un impatto dia luogo ad un salto di polo è inferiore a questo valore, qualunque sia la grandezza dell’oggetto. Relativamente indipendente dalla massa dell’oggetto è anche la probabilità che esso possa sviluppare una coppia di valore adeguato. Determinante a tal fine, infatti, è il valore del “braccio” della coppia. Se l’urto è diretto esattamente verso il centro della Terra, non si ha nessuna coppia, qualunque sia la massa e velocità dell’oggetto. Viceversa, se l’impatto è molto angolato, quasi tangente alla superficie terrestre, anche un oggetto di modeste dimensioni può sviluppare una coppia assai rilevante. Rilevante ai fini del valore del picco di accelerazione, e quindi della coppia sviluppata, dovrebbe essere anche la compattezza o meno dell’oggetto e la natura del terreno nel punto dell’impatto.

Queste variabili rendono obiettivamente impossibile una valutazione precisa della probabilità che l’urto possa sviluppare una coppia di valore adeguato. Possiamo tuttavia ragionevolmente ritenere che essa si collochi tra il 20 ed il 30% per oggetti con diametro superiore al ½ chilometro e che diminuisca velocemente al di sotto di questo limite.

 

Gli oggetti Apollo

 

Le probabilità che la Terra venga colpita da un oggetto avente una grandezza dell’ordine del mezzo chilometro sono piuttosto elevate, valutabili nell’ordine di diversi impatti ogni 100 mila anni. Responsabile di ciò è una categoria di oggetti celesti che gli astronomi chiamano col nome di “Oggetti Apollo”, applicato ad una classe  di asteroidi, il cui perielio (cioè il punto orbitale più vicino al sole) si trova all'interno dell'orbita della Terra.

Il primo di questi oggetti fu scoperto nel 1932, da Reinmuth, e nominato Apollo, donde il nome alla categoria. Nel 1937 un oggetto simile, nominato Ermes, passò a soli 800.000 chilometri dalla Terra.

Al giorno d'oggi si conoscono all'incirca 100 oggetti Apollo del diametro di almeno 1 chilometro. Il più grande fino ad ora, Efesto, ha un diametro di 10 chilometri e fu scoperto nel 1978.. La ricerca di oggetti Apollo procede attivamente. Un gran numero di essi è stato scoperto nel 1983, grazie al telescopio IRAS, installato su satellite. Il numero di Apollo con un diametro di almeno 1 chilometro è stimato nell'ordine di almeno un migliaio.

Poiché il perielio degli Apollo giace all'interno dell'orbita terrestre, ne consegue che, grazie alla precessione delle orbite, queste vengono ad intersecare periodicamente l'orbita terrestre. In questa occasione c'è effettivamente una possibilità di impatto, la cui probabilità viene valutata nell'ordine di 5.10 ^-9 all'anno per ciascun singolo Apollo.

Valutando il numero di oggetti con un diametro superiore a 1 chilometro in circa 1000, si ha una probabilità di 4 impatti ogni milione di anni. Questa probabilità cresce esponenzialmente col diminuire del diametro degli oggetti, fino a divenire di un impatto ogni pochi secoli per oggetti di 100-200 metri di diametro.

La probabilità calcolata concorda, in quanto ordine di grandezza, con la statistica degli impatti subiti dalla Terra negli ultimi 600 milioni di anni (G.W. Wetherill, “Gli Oggetti Apollo”,  Scientific American ,Maggio 79 - Tom Gehrels, “Collision with comets and asteroids”, Scientific American, march 96) . Se la Terra fosse priva di oceani e atmosfera presenterebbe una superficie butterata di crateri come quella della luna e di Mercurio. Sul nostro pianeta, invece, i processi di erosione e sedimentazione cancellano rapidamente le tracce degli impatti meteoritici. Ma in zone particolari, come ad esempio lo scudo canadese, che sono state recentemente raschiate dai ghiacci, le tracce degli antichi impatti sono state rimesse a nudo ed è possibile quindi farne una conta precisa. Sulle base di esse G. W. Wetherill ha valutato  che il pianeta, negli ultimi 600 milioni di anni, sia stato colpito da almeno 1500 oggetti aventi un diametro superiore ad un  chilometro; in buon accordo, quindi con le stime calcolate.

 

Fenomeni che si verificano durante un “salto” di poli

 

L’effetto distruttivo diretto di un impatto con un oggetto Apollo è di per se stesso devastante. Gehrels calcola che un asteroide del diametro di un chilometro che colpisse la Terra ad una velocità di 20 chilometri al secondo libererebbe un’energia equivalente a quella decine di milioni di bombe atomiche tipo Hiroshima.

Ma per quanto devastanti, questi effetti diretti sono pur sempre limitati e non sono neppure lontanamente paragonabili agli effetti distruttivi di un salto di polo. Vediamo qualitativamente di che si tratta.

Supponiamo che la Terra sia stata colpita da oggetto e che le condizioni per un salto di polo si siano verificate. Possiamo valutare qualitativamente la natura dei fenomeni che si verificano in base all’entità degli aggiustamenti necessari, a riformare i rigonfiamenti equatoriali simmetricamente intorno al nuovo asse di rotazione e a ristabilire quindi l'equilibrio isostatico.

Alcune aree della crosta terrestre sarebbero sollecitate verso l'alto,  altre verso il basso. Per ristabilire l’ellissoide intorno ad un asse spostato di una ventina di gradi sarebbero necessari aggiustamenti differenziati da zona a zona, con massimi dell'ordine dei 3/4 chilometri. Insignificanti, rispetto al diametro terrestre, ma assai rilevanti per quanto riguarda la crosta stessa. Sappiamo che i meccanismi tendenti a ristabilire l'equilibrio isostatico della crosta terrestre sono piuttosto efficaci. Quindi non c'è dubbio che dopo un certo tempo l'equilibrio isostatico sarebbe ristabilito intorno al nuovo asse di rotazione, con poli ed equatore diversi.

Il problema cruciale è sapere quanto tempo sarebbe necessario per ristabilire tale equilibrio. Sappiamo che gli strati superficiali, quando vengono sottoposti a tensioni che superano un certo limite si spezzano, scaricando la tensione in modo improvviso, "istantaneo", e provocando un terremoto. In una situazione come quella ipotizzata, si avrebbero inizialmente soltanto spostamenti di liquidi, con un aumento molto lento e graduale della velocità di rotazione intorno al nuovo asse. Quando quest’ultima raggiunge un certo valore critico dovrebbero iniziare fenomeni di "aggiustamento" del mantello e da questo momento in poi il processo dovrebbe subire una brusca accelerazione e dovrebbe completarsi in un tempo molto breve.

Giorni, ore? Difficile dirlo. Una simulazione con un modello matematico dovrebbe dare in questo caso risposte abbastanza attendibili, almeno come ordine di grandezza. Il processo di “aggiustamento” dei rigonfiamenti equatoriali dovrebbe avere un andamento esponenziale: dopo un picco iniziale molto accentuato, si dovrebbe smorzare rapidamente; ma fenomeni di assestamento dovrebbero continuare a lungo, mano a mano che l’equilibrio isostatico viene ristabilito in modo sempre più fine.

E’ ovvio che aggiustamenti dell’ellissoide terrestre di questa entità non possono avvenire senza che si verifichino ampie fratture nella crosta e nel mantello, le quali provocherebbero terremoti tali da far impallidire i più rovinosi terremoti di oggigiorno. E dalle fratture, specie quelle oceaniche, si avrebbero effusioni laviche imponenti. Un improvviso fortissimo risveglio dell'attività vulcanica in tutte le aree soggette a tensione sembrerebbe pure inevitabile.

L’inizio della deformazione del mantello, oltre che ai terremoti e all’attività vulcanica, dovrebbe dare il via ad un immane uragano su tutti i continenti, con venti violentissimi e piogge torrenziali. Una gigantesca valanga d'acqua si abbatterebbe sulle valli e le pianure di tutto il mondo.  L'acqua degli oceani e l'atmosfera, infatti, seguono, nel loro complesso, il movimento di rotazione della Terra; ma non sono vincolati rigidamente ad essa.  Se la Terra dovesse cambiare improvvisamente la direzione della propria rotazione, esse inizialmente continuerebbero per inerzia nel loro vecchio moto; solo dopo un certo tempo l'attrito con la superficie solida le porterebbe a seguire il nuovo movimento.

Su tutte le terre emerse si scatenerebbero immediatamente venti uraganici, con punte di velocità dell’ordine delle centinaia di chilometri all'ora. L'acqua degli oceani giocherebbe un ruolo assai più importante agli effetti distruttivi.  Se si devia bruscamente il moto di una bacinella piena d'acqua, si vede che il livello cresce su un lato e diminuisce sull'altro.  Qualcosa di analogo deve accadere sulla Terra. Dobbiamo aspettarci forti fluttuazioni del livello marino in varie parti del mondo. E' presumibile che si abbia una sorta di enorme onda di marea, dell'ordine di decine  e forse anche centinaia di metri, muoventesi lentamente intorno al globo.

 

Analogo ragionamento vale per il nucleo interno della Terra. Essendo liquido, continuerebbe inizialmente nel suo moto precedente, con forti attriti nella zona di contatto con il mantello. E' ovvio che a lungo andare anche il moto del nucleo liquido si allineerebbe a quello del mantello, ma attraverso turbolenze e transitori che potrebbero avere effetti importanti. Il nucleo, infatti, secondo le ultime teorie sarebbe sede di correnti elettriche responsabili del magnetismo terrestre. Queste turbolenze avrebbero indubbiamente un'influenza sul campo magnetico e potrebbero anche essere in grado di rompere determinati equilibri, provocando inevitabilmente perturbazioni nel campo magnetico che potrebbero portare anche ad una inversione dei poli magnetici.

 

Un fattore non trascurabile per valutare le condizioni climatiche successive al salto di poli, è l’inclinazione che il nuovo asse di rotazione viene ad assumere rispetto all’eclittica, la quale ha un’influenza formidabile sul clima.

Secondo il meccanismo prospettato l’asse di rotazione che la Terra assume al momento dell’impatto dovrebbe essere parallelo alla direzione dell’urto. Quale sia l’effettiva direzione che il nuovo asse viene ad avere una volta stabilizzato, è impossibile saperlo. Certamente non sarà la stessa che aveva in precedenza, a meno di un caso fortuito. Questo significa che il regime delle stagioni dopo un salto di poli sarebbe con tutta probabilità diverso da quello precedente.

Supposto, ad esempio, che l’asse di rotazione sia quasi verticale rispetto all’eclittica, si avrebbe un enorme accumulo di ghiacci alle alte latitudini e sulle montagne, con conseguente abbassamento del livello dei mari. Per contro il clima sarebbe molto più costante di oggi, con differenze climatiche stagionali limitate ed un ciclo vegetativo continuo. Questo comporterebbe la rottura delle barriere climatiche esistenti oggi, con diffusione di specie animali tropicali verso le zone polari e viceversa. Si avrebbe anche il massimo sviluppo possibile delle comunità ecologiche.

Questa sembra appunto la situazione esistente nel pleistocene, quando si aveva la presenza di formidabili calotte glaciali nel Nord America e nel Nord Europa, e di immensi ghiacciai su tutte le zone montuose del pianeta. Ma immediatamente al limite di queste masse di ghiaccio prosperava una delle più imponenti comunità zoologiche di tutti i tempi. La Siberia e l’Alaska erano percorse allora da decine di milioni (più di 40 milioni, secondo  F.C. Hibben) di mammut, animali di grossa taglia quali oggi si trovano soltanto in aree subtropicali, o comunque tali per cui l’approvvigionamento di foraggio è garantito per tutta la durata dell’anno.

Urta contro il senso comune che proprio in corrispondenza di un’era glaciale, sia esistita, proprio in quelle che oggi sono considerate le zone più inospitali del globo per le loro condizioni climatiche estreme, una delle più grandi comunità ecologiche dal tempo dei dinosauri.

Insieme ai mammut, infatti, c’erano decine di altre specie animali oggi in gran parte estinte. Di esse possediamo non solo innumerevoli scheletri e perfino esemplari intatti, conservati nel permafrost artico, ma anche un gran numero di rappresentazioni grafiche, conservate nelle grotte paleolitiche, la più antica delle quali , la grotta Chauvet in Francia, risale a circa 30 mila anni fa, nel bel mezzo del periodo glaciale. Si rimane senza fiato di fronte alla bellezza e realismo di quei dipinti. Grandi ignoti artisti hanno saputo rendere con pochi tratti sicuri fin i più piccoli particolari di quel mondo animale che popolava allora le pianure dell'Europa centrale (e che era poi lo stesso che popolava Siberia ed Alaska). Ma in quell'armonia di forme e di movimenti c'è qualcosa di stridente per la sensibilità di un  moderno zoologo. E' che proprio non si riesce ad immaginare a quale strano tipo di ambiente ecologico possa appartenere una fauna così variata. Troviamo la renna accanto al rinoceronte, il mammut, con il suo manto lanoso, accanto all'ippopotamo, l'orso accanto al leone, il leopardo con il cavallino di Brezalwski. E c’erano inoltre castori e bradipi giganti, cervi dalle grandi corna, cammelli, tigri dai denti a sciabola e molti altri ancora.

E' un mix-up che lascia sconcertati e perplessi. Fauna artica e fauna tropicale assieme, nella stessa pianura, in perfetto equilibrio con l'ambiente. Un mondo così straordinariamente ricco da un punto di vista faunistico mal si concilia con qualunque idea ci siamo fatti fino ad ora delle condizioni climatiche durante il periodo glaciale. E non troverebbe posto nel mondo di oggi.

Questa comunità è improvvisamente scomparsa alla fine del Pleistocene, quando, secondo le teorie correnti, le condizioni climatiche avrebbero dovuto migliorare.

Un salto di polo verificatosi 11.600 anni fa, con i conseguenti fenomeni distruttivi, sembrerebbe in grado di spiegare in maniera coerente e completa la situazione climatica esistente prima di questa data e la situazione che si è venuta a creare in seguito.

 

 

 

                                 Flavio BARBIERO

 

 

 

 

 

Calcoli eseguiti dal Dot.. F.L. Gallen, direttore del “Department of Commerce U.S. Coast and Geodetic Survey”,Washington

 

Siano le equazioni della sfera e dell’ellissoide di rotazione rispettivamente:

1)     x²  + y² +  z²  = b²

2)    

dove l’asse y è l’asse di rivoluzione. Sia dM la massa dell’anello generato dalla rotazione del rettangolo dxdy intorno all’asse y. Avremo:

3)     dM = 2pdx dxdy

dove d è la densità. Per ogni particella dell’anello l’accelerazione centrifuga è la stessa, ed è uguale ad w² x, dove w è la velocità angolare in radianti al secondo.

La forza centrifuga dF esercitata dall’anello è data quindi dalla:

4)     dF =  w²x dM =  2pdw²x² dxdy

 

Integrando l’equazione 4) rispetto ad x ed y avremo:

                          

5)           

 

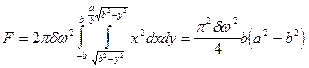
Nell’espressione 5) F è espresso in dine, quando  d è in grammi per centimetro cubo e a e b in centimetri. La quantità  w  può essere sostituita con  2pn, dove n è il numero dei giri per secondo. La Terra esegue un giro completo mediamente in 86.164,09 secondi solari, per cui  n = 7,28 10^-5.

 

Calcolo della forza centrifuga effettuato dal Dott. Deininger (Smith College) sulla base della formula di Gallen

 

Calcolo della forza centrifuga prodotta dalla forza rotazione dei rigonfiamenti equatoriali:

A.   Dati essenziali:

La formula 5) è applicata considerando lo spessore del rigonfiamento di 13,3443 miglia all’equatore, in diminuzione graduale fino ad annullarsi ai poli.

Nell’eseguire i calcoli, il Dott. Deininger è stato richiesto di sottrarre tre miglia dallo spessore del rigonfiamento, per tenere conto dell’acqua degli oceani, che non fornisce alcun contributo alla coppia di stabilizzazione (in virtù dell’equilibrio isostatico, sarebbe più appropriato sottrarre il peso dell’acqua, anziché il suo volume; l’approssimazione, tuttavia, appare accettabile)

Calcolo:

1)    

 

dove       s           =          densità in gr/cm³

               a          =          raggio terrestre all’equatore in cm

   b          =          raggio terrestre ai poli in cm

               w         =          2 - n  r  =  rps

 

2)           F    =   p⁴sn². b(a³ - b³)

dove       s           =          2,7 gm/cm³

               n          =          1/86.164

               b          =          6,402 . 10⁸  cm

               a          =          6,4165 . 10⁸ cm

3)            F  =     4,0368 . 10²⁵  dine  = 4,1192. 10¹⁹  kg.

n  Charles Hapgood, “The Path of the Pole”, Chilton Book Co, Philadefphia, 1970

n  R. F. Deimel, “Mechanics of the gyroscope. The dinamics of rotation”, Dover Edition, 1950

n  G.W. Wetherill, “ The Apollo objects”’Scientific American, May 79

n  Tom Geherels, “Collision with Comets and Asteroids”’ Scientific American, March 96

n  E. Spedicato, “Apollo objects, Atlantis and the deluge: a catastrophical scenario for the end of the last glaciation”, Quad. 90/22, 1990, Bergamo University, Italy