CAMBIAMENTI
DELL’ASSE DI ROTAZIONE TERRESTRE
DOVUTI AD IMPATTI
DI ASTEROIDI/COMETE
E LORO EFFETTI
GEOLOGICI
Le crisi geologiche ricorrenti
La storia geologica della Terra è caratterizzata da lunghi periodi di stabilità, inframmezzati da crisi brevissime e violente, durante le quali si hanno da un lato imponenti eruzioni vulcaniche, orogenesi, cambi climatici, inversioni del campo magnetico, variazioni del livello marino ecc; dall’altro estinzioni di massa, emergenza di nuove specie, cambio radicale degli equilibri ecologici.
|
|
|
|
Le grandi estinzioni di massa che si sono verificate periodicamente nel passato, interessando sia la terraferma che gli oceani. La lunghezza della freccia indica la quantità di specie scomparse. La più grave si è verificata all’inizio del Perminao, quando il 95% delle specie si è improvvisamente estinto. A destra una tipica sequenza stratigrafica geologica. Ogni strato indica condizioni climatiche stabili, che cambiano in maniera repentina e radicale, dando origine ad un nuovo strato di diversa composizione |
|
Le geologia non è ancora in grado di fornire una spiegazione di queste crisi ricorrenti. Vista la contemporaneità di questi fenomeni sono state avanzate ipotesi che esistano relazioni di causa ed effetto fra alcuni di essi; ma non sempre è evidente quale sia la causa e quale l’effetto.
Negli ultimi anni si sta affermando l’ipotesi che le estinzioni animali siano dovute a catastrofici impatti con comete o asteroidi, perché per alcune di esse, come ad esempio quella del cretacico superiore, che vide l’estinzione in massa dei dinosauri e preparò l’avvento dei mammiferi, si è potuto appurare la coincidenza con la caduta di un grande asteroide. Coincidenze con l’impatto di un asteroide sono state riscontrate anche in altre estinzioni animali, per cui il rapporto di causa-effetto appare sempre più probabile.
Coincidenze, però sono state rilevate anche fra estinzioni e variazioni del livello marino, ed anche tra estinzioni e manifestazioni di vulcanismo estreme, come la grande colata vulcanica del Deccan, avvenuta alla fine del cretacico, per cui vari autori hanno avanzato l’ipotesi di un rapporto di causa-effetto fra questi fenomeni e le estinzioni animali.
Ma nessuno è riuscito a dimostrare in modo convincente come fenomeni di natura locale e tutto sommato limitata abbiano potuto produrre catastrofi ecologiche a livello globale.

Tabella riassuntiva di fenomeni geologici osservati in coincidenza con le principali estinzioni del passato
Ma soprattutto nessuno è stato in grado di spiegare quale sia la causa ultima che determina lo scatenarsi contemporaneo di tutti questi fenomeni; perché deve esserci per forza una causa che scatena queste ricorrenti crisi geologiche.
La tesi che mi propongo di dimostrare qui di seguito è che tutte queste crisi sono iniziate da improvvisi spostamenti dei poli, provocati da impatti sulla Terra di comete e asteroidi.
Effetti catastrofici degli impatti
La contemporaneità è un fattore importante per stabilire un rapporto di causa effetto fra estinzioni ed impatti, ma il problema è spiegare come oggetti relativamente piccoli (3 km è il diametro ritenuto sufficiente perché un asteroide sia in grado di provocare un’estinzione di massa a livello planetario) possano avere effetti catastrofici sull’intero pianeta.
Secondo le stime di Tom Gehrels (vedi: Tom Gehrels, “Collision with comets and asteroids”, Scientific American, March 96), un asteroide del diametro di 1 chilometro, che colpisca la Terra ad una velocità di 20 km al secondo, libererebbe un’energia equivalente a 10 miliardi di bombe atomiche tipo Hiroshima. L’energia liberata da un asteroide di 3 km dovrebbe essere cento volte superiore.
Ma per quanto devastanti a livello locale, questi effetti diretti non sono sufficienti da soli a giustificare estinzioni di massa e processi geologici di natura diversa a livello planetario. Paragonato alla Terra, un asteroide del diametro di 3 chilometri è come una minuscola sfera di 7mm di fronte ad una palla di 25 metri. La sua massa è assolutamente trascurabile e non è evidente come possa provocare effetti catastrofici a livello mondiale. A maggior ragione spiegare come possano innescare a livello planetario fenomeni come vulcanismo, orogonesi, moti convettivi del Sima, regressioni, inversioni del magnetismo e cambiamenti climatici permanenti.
|
Paragonato alla Terra un asteroide di 3 km di diametro è come una minuscola sfera di 7 millimetri (in alto a destra) di fronte ad una palla di 25 metri. La sua massa è irrilevante e non può provocare direttamente effetti catastrofici a livello globale, compreso il fondo di tutti gli oceani.
|
|
L’ipotesi più accreditata è che l’impatto possa provocare una repentina diminuzione della temperatura ed altre perturbazioni climatiche su tutto il mondo, a causa dei materiali iniettati nell’atmosfera. Ma anche in tal caso è difficile giustificare l’entità degli effetti. La quantità di materiali immessi nell’atmosfera è stimata intorno a 100 volte la massa dell’asteroide impattante.
Per un asteroide di 3 km la quantità di materiali immessi nell’atmosfera dovrebbe essere dell’ordine di quella immessa dalla più grande eruzione vulcanica recente, avvenuta a Tambora (Indonesia) nel 1815. Quella eruzione, in effetti, ebbe una qualche influenza sul clima terrestre, perché l’estate successiva fu insolitamente fredda su tutto l’emisfero settentrionale (vedi: Stommel H. and Stommel E.: The year without a summer, Scientific American, 1979). Ma non si può certo parlare di catastrofe a livello mondiale: si trattò di una semplice “increspatura” del clima, che provocò soltanto temporanee difficoltà ad un numero limitato di individui.
Certamente non fu una catastrofe globale e inoltre non fu registrato alcun effetto sugli oceani. Un impatto di una asteroide o di una cometa avrebbe senza dubbio effetti devastanti, ma l’ampiezza dell’area direttamente interessata potrebbe essere al più dell’ordine dei milioni di chilometri quadrati, una percentuale trascurabile della superficie terrestre.
Le estinzioni di massa del passato, invece, e i fenomeni geologici associati sono stati globali, avendo interessato non solo tutti i continenti, ma anche l’insieme degli oceani, sia in superficie che in profondità. Questo è impossibile da giustificare come un effetto diretto dell’impatto, anche ammesso che si sia verificato in mare aperto. (Ma l’asteroide che ha prodotto il cratere di Chicxulub e che viene ritenuto la causa dell’estinzione dei dinosauri, ad esempio, ha colpito la Terra in un bacino chiuso come il Golfo del Messico.)
L’unico modo, a mio aviso, per spiegare gli effetti globali di un impatto è quello di ritenere che esso sia in grado di provocare uno spostamento praticamente istantaneo dell’asse di rotazione terrestre, vale a dire uno spostamento dei poli. Vedremo come questo sia possibile.
Prove che i poli si sono spostati rispetto alla posizione attuale
|
É ben noto il fatto che i poli hanno cambiato sovente la loro posizione sulla superficie terrestre nel corso delle passate ere geologiche. I segni lasciati dalle calotte glaciali in Africa e India, il magnetismo residuo nelle rocce, la distribuzione di antiche barriere coralline e dei depositi di carbone e così via, costituiscono nel loro insieme una prova assoluta che i poli hanno girovagato dall’equatore fino alla posizione attuale. Le teorie attuali attribuiscono questi spostamenti alla deriva dei continenti e a spostamenti superficiali di grandi quantità di materiali, dovuti ai processi di erosione e sedimentazione, che sarebbero in grado di produrre lentissimi spostamenti dei poli: pochi centimetri all’anno, al massimo, ma in milioni di anni possono accumulare spostamenti di migliaia di chilometri. |
Lo spostamento del polo nord nel corso degli ultimi 300 milioni di anni |
Perché si verifichino i fenomeni descritti, però, è necessario che la variazione sia praticamente “istantanea” in scala geologica. Anche dalla figura di cui sopra (tratta da un libro di testo dell’Università di Pisa) sembrerebbe che lo spostamento del polo sia stato non continuo, ma sia avvenuto per salti.
Esistono indicazioni consistenti che l’ultimo salto si sia verificato in un passato recente ed abbia segnato la fine del periodo geologico chiamato Pleistocene..
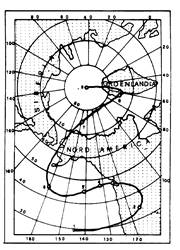
La posizione del polo nord durante il Pleistocene
|
Tra i 50 e i 12 mila anni or sono una enorme calotta glaciale, spessa oltre tre chilometri, si era irradiata dall’area di Hudson, nel Canada orientale, fino a raggiungere verso sud l’attuale latitudine di New York e verso ovest i ghiacciai che scendevano dalle montagne rocciose, in Alaska. Nello stesso periodo il Nord Europa era coperto da calotte glaciali che al culmine della loro espansione raggiunsero le latitudini di Londra e Berlino. La quantità di acqua congelata sulla terraferma era talmente grande, che il livello del mare era sceso di oltre 100 metri rispetto ad oggi. |
Posizione della calotta polare durante il Pleistocene |
Le teorie attuali, numerose e spesso in contrasto tra loro, cercano di spiegare l’esistenza di queste masse di ghiaccio, eccentriche rispetto ai poli odierni, con il fatto che il clima fosse allora assai più freddo su tutta la Terra.
|
40 milioni di mammut vagavano per le pianure della Siberia e dell’Alaska, ed insieme ad essi c’erano renne, rinoceronti, cavalli, ippopotami, orsi, leoni, leopardi, castori, bradipi giganti, cervi dalle grandi corna, cammelli, tigri dai denti a sciabola e molti altri ancora. Prova certa che il clima siberiano era allora di gran lunga più mite e costante di quanto lo sia attualmente. |
Fauna plestocenica (grotto Chauvet) |
La spiegazione più logica e naturale per questa situazione climatica, tanto che è stata la prima ad essere avanzata nel 19.mo secolo, è che i poli si trovassero allora in una posizione diversa rispetto ad oggi. Si sarebbero spostati nella posizione attuale alla fine del Pleistocene.
Tutti i metodi impiegati per accertare la posizione dei poli nel passato forniscono punti discreti, non spostamenti lenti e continui, suggerendo l’idea che i poli si spostino per “salti” discreti. Pertanto i “salti” di poli dovrebbero essere un fenomeno ricorrente e piuttosto frequente nella storia della Terra e dovrebbero costituire quella causa ultima che scatena le ricorrenti crisi geologiche di cui si è detto.
Rimane ora da scoprire quale sia la causa che provoca un subitaneo spostamento dei poli. Si è detto che l’unica possibile dovrebbe essere l’impatto di un asteroide o di una cometa. Visto il rapporto fra le dimensioni della Terra e quelle di una grande asteroide (25 metri contro 7 millimetri), questo potrebbe sembrare a priori impossibile; una analisi accurata del problema, però, mostra che al contrario questo è un evento praticamente inevitabile.
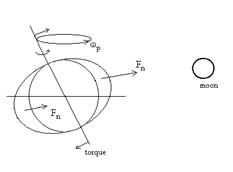
La Terra è un pianeta intrinsecamente instabile, al punto che un semplice urto (vedremo fra poco con i calcoli quanto piccolo) è sufficiente ad innescare un processo che nel giro di pochi giorni (o al massimo settimane e cioè praticamente istantaneo in scala geologica), può provocare uno slittamento permanente del pianeta rispetto al proprio asse di rotazione (e di conseguenza uno slittamento del poli) di grande ampiezza, anche dell’ordine delle decine di gradi (il che significa uno spostamento dei poli dell’ordine delle migliaia di km).
Inoltre questo spostamento comporta normalmente anche una variazione dell’inclinazione dell’asse di rotazione rispetto all’eclittica.
Sulla possibilità di rapidi spostamenti dei poli
L’ipotesi che l’inclinazione dell’asse terrestre rispetto all’eclittica e che la posizione dei poli rispetto alla Terra possano variare è stata presa in considerazione fin dal secolo 19.mo.
Alcuni fra i maggiori scienziati dell’epoca, fra cui J.C. Maxwell e Sir George Darwin (figlio del più celebre Charles Darwin), si sono occupati del problema, arrivando alla conclusione che l’effetto stabilizzante dei rigonfiamenti equatoriali terrestri è talmente grande, che non c’è forza ipotizzabile in grado di provocare uno spostamento dell’asse di rotazione rispetto al pianeta stesso, a meno di una “collisione planetaria”. Essi pertanto hanno scartato l’idea di uno spostamento dei poli come impossibile ed in pratica non meritevole di discussione.
La loro influenza è stata talmente decisiva, che nessuno, fino ad oggi, ha preso in considerazione tale ipotesi. Anche la possibilità della variazione dell’inclinazione dell’asse rispetto all’eclittica viene negata, in virtù del principio della dinamica che vuole che in un sistema isolato il momento della quantità di moto rimanga invariato.
Su una cosa Maxwell (e con lui tutti i matematici e i fisici) aveva ragione è cioè che la stabilità della Terra è dovuta esclusivamente ai suoi rigonfiamenti equatoriali. Se la Terra fosse un corpo perfettamente sferico ed omogeneo, una singola persona, camminando sulla sua superficie, sarebbe sufficiente a far spostare i poli in qualsiasi direzione e per qualsiasi ampiezza.
Anche i calcoli da lui eseguiti, ovviamente, erano corretti; ma purtroppo non tenne conto (né lo poteva, non avendo gli ingegneri navali ancora scoperto l’effetto destabilizzante delle superfici liquide libere) della presenza sulla Terra di una enorme superficie liquida libera, qualcosa come 350 milioni di kmq, che la rende intrinsecamente instabile.
Un semplice tsunami di qualche metro di altezza, come quello verificatosi in Asia qualche anno fa, è sufficiente a spostare in maniera sensibile l’asse di rotazione. Se una enorme ondata, dell’ordine delle centinaia di metri si muovesse dall’equatore verso i poli, l’asse di rotazione si sposterebbe di parecchi gradi, con conseguenze imprevedibili.
Inoltre Mawell, non conoscendo la composizione interna della Terra, la considerava come un corpo completamente solido e non come una sfera composta da strati concentrici alternativamente liquidi e solidi. I calcoli sono ben diversi nei due casi. In effetti il momento della Terra può cambiare, ed in effetti cambia istante per istante, sia in quantità che in direzione, a causa della sua struttura interna e del movimento di precessione.
Anche l’affermazione che l’inclinazione dell’asse rispetto all’eclittica non può cambiare è palesemente errata. Innanzitutto perché la Terra non è un sistema isolato, un piccolo astro come la luna è quasi interamente responsabile del fenomeno della precessione, che provoca una variazione veramente ampia e continua della direzione dell’asse rispetto alle stelle fisse. Anche l’inclinazione dell’asse rispetto all’eclittica cambia ciclicamente di qualche grado a causa del fenomeno della nutazione.
|
Il movimento di precessione è dovuto alla forza gravitazionale esercitata dal sole e più ancora dalla luna sui rigonfiamenti equatoriali. Ne risulta una coppia perturbatrice che è dell’ordine di milioni di volte più piccola di quella stabilizzatrice sviluppata dai rigonfiamenti stessi. Una coppia apparentemente insignificante, che tuttavia ha un’influenza enorme sul momento della Terra, a causa della composizione di quest'ultima.
|
|
Vediamo perché.
|
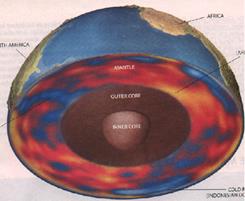
La Terra è costituita da un nucleo solido, del diametro di 2780 km, seguito da un involucro liquido, anch’esso metallico, di 2.080 km, ed in fine da un guscio di roccia “solida” di 2.900 km, in cima al quale c’è un sottile strato di acqua. Lo strato metallico liquido separa le due parti solide e in questo modo impedisce qualsiasi trasmissione diretta di moto fra loro. |
|
L’attrazione gravitazionale del sole e della luna responsabile della precessione agisce esclusivamente sul guscio solido esterno, non sullo strato metallico liquido e sul nucleo interno. Il movimento di precessione, pertanto, interessa soltanto il guscio esterno.
Ovviamente esso induce, per attrito, una corrente di trascinamento nello strato metallico liquido che sta a contatto, per cui alla fine le variazioni di moto dovute alla precessione si trasmettono anche al nucleo centrale, ma con enorme ritardo. Viste le masse in gioco ed il meccanismo di trasmissione del momento angolare, questo ritardo è certamente dell’ordine delle migliaia di anni, o probabilmente di più.
|
In teoria, quindi, a causa del movimento di precessione, l’asse di rotazione del nucleo centrale può divergere rispetto a quello dello strato esterno, nell’attuale situazione, fino ad un massimo di 46 gradi. E quello dello strato liquido intermedio, nel suo complesso, di ben più di 20 gradi. |
|
In scala minore, anche l’asse di rotazione degli oceani nel loro complesso non coincide con quello del guscio esterno, a causa delle correnti oceaniche.
Se ne deve concludere che la direzione del momento angolare della Terra, considerata nel suo insieme, è certamente assai diversa da quella dell’asse di rotazione del suo guscio esterno e cambia direzione ad ogni istante, perché i quattro gusci concentrici si muovono indipendentemente l’uno dall’altro. Anche la quantità del momento angolare diminuisce costantemente, perché l’attrito che si esercita fra i vari gusci inevitabilmente dissipa energia.
La precessione come causa di periodi riscaldamenti e raffreddamenti della superficie terrestre
Il principio di conservazione del momento angolare è applicabile soltanto ad un sistema isolato che non emetta materia o energia di qualsiasi tipo. Nel caso della Terra, il fatto l’asse di rotazione del guscio esterno cambi continuamente direzione a causa della precessione, induce turbolenza nello strato liquido sottostante con conseguente dissipazione di energia sotto forma di calore (e probabilmente di campo magnetico), a spese del momento angolare. Pertanto esso provoca una variazione del momento globale della Terra, sia in quantità che in direzione.
Con l’attuale angolo di precessione, la divergenza fra l’asse di rotazione del guscio esterno e quello del nucleo centrale può variare periodicamente da 0 a 46 gradi. Tanto più grande è l’angolo fra i due assi, tanto maggiore sarà la quantità di energia dissipata e quindi tanto maggiore il calore irradiato attraverso lo strato esterno. La precessione, quindi, è certamente causa di un periodi riscaldamento e raffreddamento della superficie terrestre, a causa della periodica variazione dell’ampiezza dell’angolo fra l’asse di rotazione esterno e quello del nucleo interno.
Come ipotesi estrema, se l’asse di rotazione esterno fosse invertito rispetto a quello del nucleo interno (cosa in teoria del tutto possibile), il momento angolare di entrambi sarebbe dissipato in calore, a causa dell’attrito con lo strato liquido intermedio.
Questo è quanto molto probabilmente è accaduto a Venere, un pianeta che dovrebbe avere una velocità di rotazione simile a quella della Terra e di Marte ed una superficie più o meno della stessa età. Invece la rotazione di Venere è quasi nulla e la sua superficie attuale si è solidificata quasi quattro miliardi di anni dopo. Per qualche ragione (che vedremo meglio nel seguito) il guscio esterno ed il nucleo centrale di questo pianeta devono essere entrati in controrotazione, dissipando reciprocamente il loro momento angolare; il calore sviluppato in questo processo deve essere stato sufficiente a fondere completamente il pianeta.
In che modo i poli possono spostarsi
In conclusione l’affermazione che l’asse di rotazione possa cambiare direzione soltanto se la Terra viene colpita da un corpo avente le dimensioni di un pianeta come Marte è totalmente priva di fondamento.
Parimenti errata è l’idea che una massa planetaria sia necessaria anche per avere uno slittamento dei poli, vale a dire uno slittamento dell’asse di rotazione rispetto alla terra stessa. Per ottenere questo, infatti, è sufficiente “riplasmare” i rigonfiamenti equatoriali, vale a dire indurre delle deformazioni sulla superficie del pianeta percentualmente trascurabili (lo spessore massimo dei rigonfiamenti è appena lo 0.3% del raggio terrestre, assolutamente inapprezzabile ad occhio nudo).
Si tratta ora di vedere come sia possibile riplasmare i rigonfiamenti equatoriali. Il principio non è difficile da capire, se si tiene conto che all’equatore il 30% del rigonfiamento equatoriale (percentuale che cresce mano a mano che ci si sposta verso i poli, fino a divenire preponderante) è costituito da acqua, che in teoria può essere spostata da una zona all’altra con un impiego di forze relativamente esiguo. Un’onda di marea di qualche centinaio di metri, che si muovesse dall’equatore lungo i meridiani, farebbe spostare l’asse di rotazione di parecchi gradi e di conseguenza i poli di centinaia o anche migliaia di km.
Non ci resta altro da fare, quindi, che scoprire quale meccanismo potrebbe provocare un’onda di marea di questa entità e quali conseguenze avrebbe sull’equilibrio isostatico della crosta. Ebbene, è possibile dimostrare in maniera conclusiva che impatti di comete e asteroidi sono in grado di fornire questo meccanismo..
Vista la sproporzione fra i due corpi ( in scala: 7 millimetri per un asteroide di 3 km, contro 25 metri di diametro per la Terra), la possibilità che un impatto del genere possa indurre un salto di poli sembrerebbe da escludersi a priori. La massa di un asteroide, e l’energia associata, sono assolutamente trascurabili; esse non possono in alcun modo provocare direttamente uno spostamento dei poli superiore a qualche centimetro!
Se massa ed energia dell’asteroide possono essere trascurati, non è lo stesso per la coppia perturbatrice sviluppata dall’impatto. Per capirne il perché bisogna considerare (fatto stabilito già dallo stesso Maxwell) che la coppia stabilizzatrice della Terra è sviluppata non dall’intera massa del pianeta, ma soltanto dai suoi rigonfiamenti equatoriali e cioè da un anello di materiali avente uno spessore massimo, all’equatore, di 14 chilometri.
La sproporzione fra la massa dei rigonfiamenti equatoriali e quella di un asteroide è incomparabilmente più piccola di quella esistente fra quest’ultima e l’intera massa terrestre. Pertanto, data l’alta velocità dell’asteroide (oltre 20 chilometri al secondo), la coppia impulsiva sviluppata dall’impatto può raggiungere valori di picco molto elevati, tali da superare la coppia di reazione massima sviluppabile dai rigonfiamenti equatoriali.
Per quanto elevata, tuttavia, si tratta pur sempre di una coppia impulsiva, che agisce per un tempo troppo breve per provocare effetti percettibili su un comune giroscopio, rigido e indeformabile.
La Terra, però, non è un giroscopio comune. Innanzitutto è coperta da uno strato di acqua, che introduce un elemento di instabilità, perché reagisce immediatamente ad ogni cambiamento, sia pur minimo, di moto (come la scienza delle costruzioni navali insegna, ogni “specchio liquido libero” è fonte di instabilità). In secondo luogo, anche la crosta esterna “solida” del pianeta è in realtà plastica ed è facilmente deformabile dalla forza centrifuga.
Si dimostra che, a causa di questi due fattori, una coppia impulsiva di direzione ed intensità opportune può “innescare” un processo che alla fine risulta in un cambiamento permanete dell’asse di rotazione della Terra e quindi uno spostamento dei poli.
|
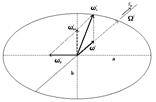
Possiamo studiare il comportamento di un giroscopio attraverso la sua “elisse di inerzia”, in un caso che non è mai stato esaminato dai matematici, da un lato per l’estrema difficoltà di farlo con equazioni matematiche, dall’altro per il suo scarso interesse pratico: quello di un giroscopio soggetto ad una coppia perturbatrice dello stesso ordine di grandezza della coppia stabilizzatrice sviluppata dai suoi “rigonfiamenti” equatoriali. Nell’appendice matematica allegata [1] si dimostra che quando la coppia perturbatrice eguaglia la coppia stabilizzatrice, l’asse di precessione diventa asse di rotazione permanete del giroscopio. Questi recupera il suo asse di rotazione originario soltanto se e quando la coppia perturbatrice si annulla completamente. |
|
|
|
Un impatto sviluppa una coppia impulsiva. Se il valore di quest’ultima supera quello massimo sviluppabile dai rigonfiamenti equatoriali, la Terra cambia istantaneamente il proprio asse di rotazione e recupera quello di partenza non appena la coppia impulsiva svanisce completamente. Se però la coppia perturbatrice non si annulla completamente, se cioè rimane una coppia residua avente lo stesso segno di quella sviluppata dall’impatto, allora la Terra conserva “memoria” dell’impatto e della sua direzione.
Questa “memoria” consiste in una componente rotazionale molto piccola, meno di un milione di volte il valore della rotazione principale. La caratteristica più importante di questa componente rotazionale, però, è che è “fissa” rispetto alla Terra.
Sotto la spinta centrifuga di questa minuscola componente rotazionale, masse di acqua cominciano a muoversi per disporsi su un cerchio massimo perpendicolare a tale rotazione e cioè la linea equatoriale da essa individuata. Mano a mano che l’acqua si sposta verso il nuovo equatore, però, la componente rotazionale responsabile del movimento cresce di valore, a spese della componente rotazionale principale; di conseguenza, la forza centrifuga che provoca lo spostamento dell’acqua aumenta, per cui si ha un maggior afflusso di acqua verso il nuovo equatore, che a sua volta provoca un aumento della rotazione e così via.
E’ un processo che inizia molto lentamente, ma che viene progressivamente accelerandosi, fino a che la forza centrifuga indotta da questa nuova componente rotazionale non diviene sufficiente a provocare la deformazione della crosta terrestre.
A questo punto si ha una improvvisa accelerazione del processo ed in breve tempo il rigonfiamento equatoriale si rimodella intorno al nuovo asse di rotazione, rendendo il movimento di rotazione della Terra nuovamente stabile.
Questo meccanismo mostra come i poli terrestri, contrariamente a quanto si è sempre postulato, possono effettuare “salti” di migliaia di chilometri nel giro di pochi giorni (il che significa quasi istantaneamente), sotto l’effetto di forze apparentemente trascurabili, come la coppia sviluppata dall’impatto di un asteroide di media grandezza.
E’ importante sottolineare il fatto che questo processo richiede necessariamente la presenza di uno strato liquido su un guscio esterno plastico, facilmente deformabile, sì da poter facilmente rimodellare il rigonfiamento equatoriale. Pertanto, in tutto il sistema solare un processo del genere attualmente è possibile soltanto sulla Terra, perché è l’unico corpo che possiede oceani liquidi su un guscio plastico. Gli altri corpi del sistema o non possiedono oceani, come Mercurio, Venere, Marte, la luna ecc., oppure non hanno una crosta solida a portata di impatto, come il sole, Giove e gli altri pianeti esterni
Cosa accade in caso di uno spostamento dei poli
Una catastrofe globale può essere giustificata soltanto se si ammette che l’impatto di un piccolo oggetto come un asteroide o una cometa sia in grado di provocare uno spostamento macroscopico dei poli in un tempo molto breve. Gli effetti di un tale spostamento sono ovviamente legati alla sua ampiezza, ma conseguenze non meno importanti sono da attribuirsi alla variazione dell’inclinazione dell’asse rispetto all’eclittica (che sono indipendenti dalla prima).
L’entità di questi spostamenti non è legata direttamente alla grandezza del corpo impattante. Anche il punto dell’impatto ha poca influenza sulle sue conseguenze. Normalmente la velocità del corpo all’impatto è molto alta, compresa fra 20 e 80 chilometri al secondo, per cui l’acqua si comporta e trasmette l’urto come una superficie solida (a questa velocità la materia di fronte al corpo impattante non ha il tempo di spostarsi di lato. Essa vaporizza all’istante, formando una tasca di gas ad altissima pressione, che alla fine esplode).
Vediamo comunque cosa accade in caso di uno spostamento dei poli:
Innanzitutto si avrebbe un veloce “rimodellamento” del rigonfiamento equatoriale intorno al nuovo asse di rotazione (a dire il vero questo rimodellamento è una condizione necessaria perché i poli si spostino, per cui non può essere considerato una “conseguenza”, ma piuttosto la causa dello spostamento: le due cose procedono necessariamente insieme di pari passo). Questo è dovuto, come si è visto, in un primo momento soltanto allo spostamento dell’acqua degli oceani e soltanto in seguito ad un aggiustamento della crosta, dovuto alla forza centrifuga.
Di conseguenza alcune aree della crosta si rigonfieranno, altre si appiattiranno, mentre altre ancora subiranno deformazioni molto contenute o del tutto nulle. Per uno spostamento dei poli di una ventina di gradi, la deformazione massima della crosta sarebbe dell’ordine di 1 km (distribuito su un arco di circonferenza di 20.000 km, il che significa una deformazione di 5 centimetri per km). Veramente piccola in confronto al diametro della Terra, ma in ogni caso con conseguenze molto importanti sulla superficie. In particolare, nelle aree dove si ha un rigonfiamento si possono verificare fratture della crosta con conseguenti terremoti molto intensi e possibilità di grandi fuoriuscite di magma.
L’improvviso spostamento in latitudine delle masse continentali, poi, provocherebbe l’insorgere di intense forze tangenziali di queste masse contro la crosta sottostante, con l’innesco di nuove celle di convezione e l’inizio di una nuova deriva continentale. Questo potrebbe dare inizio ad una nuova fase orogenetica se e dove esistessero le condizioni idonee.
Si avrebbero, ovviamente, anche variazioni delle condizioni climatiche, dovute sia allo spostamento in latitudine di larghe aree continentali, sia al cambiamento di inclinazione dell’asse rispetto all’eclittica (che ha un grandissimo effetto sul clima), con variazioni della massa delle calotte polari e di conseguenza del livello del mare.
Infine si avrebbero perturbazioni del campo magnetico terrestre, con possibili inversioni della sua polarità, dovute a cambiamenti della circolazione nello strato metallico liquido intermedio.
Effetti sulla vita – Estinzioni di massa
Gli effetti sui sistemi ecologici e sulle specie viventi dipenderanno, ovviamente, dall’ampiezza dello spostamento. Quanto maggiore lo spostamento dei poli, tanto più drammatici gli effetti. Dobbiamo tuttavia distinguere chiaramente gli effetti immediati da quelli a lungo termine.
Consideriamo uno spostamento dell’ordine di 15/20 gradi.
- Innanzitutto si avrebbe una distruzione totale nell’area direttamente interessata dall’impatto; di norma si tratta di un’area relativamente limitata, poco significativa a livello mondiale.
- Assai più devastanti saranno le ampie fluttuazioni del livello del mare che si verificano durante le prime fasi dello spostamento. In alcune zone si possono avere onde di marea di parecchie centinaia di metri, con conseguenti distruzioni in vaste aree di terraferma (ci sono evidenze che alla fine del Pleistocene il livello del mare abbia raggiunto un’altezza di 350 metri alle Haway e addirittura di 700 in Alaska)
- Altre aree della piattaforma continentale rimarrebbero a secco per qualche tempo, con conseguenti danni agli ecosistemi locali. Inoltre si avrebbe ovunque nel mondo un improvviso emergere di acque oceaniche profonde, fredde e povere di ossigeno, con drammatici effetti su tutti gli ecosistemi marittimi.
- Sui continenti, eruzioni vulcaniche e terremoti provocherebbero molte vittime. Ma le distruzioni più importanti sarebbero dovute ai venti violentissimi e alle piogge torrenziali che si scatenerebbero su tutta la Terra. L’atmosfera, infatti, segue grosso modo la rotazione terrestre, ma non è vincolata al suolo. Se la Terra cambiasse improvvisamente la direzione della propria rotazione, l’atmosfera continuerebbe in un primo momento nel suo moto originale, provocando venti uraganici e piogge eccezionali su tutto il pianeta. Si verificherebbero quindi catastrofiche alluvioni su tutti i continenti, con massicce distruzioni di flora e fauna. (milioni di animali sarebbero ammassati dall’acqua in bacini chiusi e coperti di fanghiglia, trasformandosi in fossili per la delizia dei paleontologi futuri).
- L’effetto combinato di tutti questi fenomeni provocherebbe necessariamente un generale raffreddamento del clima terrestre, che sarebbe comunque temporaneo e probabilmente con effetti non così drammatici come prospettato dal molti geofisici.
Cambiamenti climatici permanenti
La immediate distruzione di flora e fauna può essere importante, ma normalmente non al punto di provocare direttamente l’estinzione di un elevato numero di specie. Se le condizioni ambientali, dopo il salto di poli, si ristabiliscono come per l’innanzi, le specie recuperano velocemente e ricostituiscono i precedenti ecosistemi con varianti non troppo significative.
Spesso, però, le condizioni climatiche risultano radicalmente diverse da prima. Un “salto” di poli comporta normalmente uno slittamento delle fasce climatiche, lo scioglimento delle calotte polari e la formazione di altre. Comporta anche un cambiamento dei venti dominanti e delle correnti oceaniche, con ulteriori variazioni climatiche.
Se però l’inclinazione dell’asse di rotazione sull’eclittica rimane più o meno la stessa, tutto ciò provoca soltanto una migrazione di specie da una località all’altra. Ostacoli naturali e temporanee difficoltà possono provocare l’estinzione di un certo numero di specie incapaci di migrare, ma quelle dominanti, che occupano vaste aree, non dovrebbero avere problemi di sopravvivenza.
Ben diverso è il caso in cui l’inclinazione dell’asse subisca una variazione importante. Un elemento chiave per valutare le condizioni climatiche dopo un salto di poli è l’inclinazione che l’asse assume dopo un salto di poli; questa, infatti, ha un forte effetto sui cambiamenti climatici stagionali, sull’accumulo di ghiacci e sulla distribuzione della flora e della fauna.
Un alto valore del “tilt” (inclinazione dell’asse) comporta inverni lunghi e freddi, seguiti però da estati molto calde. In queste condizioni ci sarebbe un accumulo di ghiacci molto ridotto, perché la neve invernale sarebbe sciolta dalle alte temperature estive a qualsiasi latitudine e altezza. Pertanto le calotte polari e i ghiacciai montani sarebbero ridotti al minimo ed il livello del mare salirebbe. La flora e la fauna sarebbero fortemente dipendenti dalla latitudine, perché il numero di specie in grado di superare i rigori invernali (o quelli estivi) diminuirebbero con la latitudine.
Per contro, un piccolo valore del “tilt” provocherebbe un enorme aumento del ghiaccio alle alte latitudini e sulle montagne, perché durante l’estate ci sarebbe uno scioglimento molto limitato delle nevi invernali. D’altra parte, però, il clima sarebbe molto più stabile che non al giorno d’oggi, con differenze climatiche stagionali molto ridotte e interruzioni nella crescita dei vegetali di breve durata. Questo provocherebbe l’abbattimento delle barriere climatiche attuali, con conseguente migrazione di specie tropicali verso le regioni nordiche e viceversa.
Queste variazioni, insieme all’iniziale drastica riduzione del numero di individui sopravvissuti, comporterebbe profondi cambiamenti negli ecosistemi, e quindi la possibilità di estinzione totale di specie non adattate alle nuove condizioni e l’aumento esplosivo di altre meno specializzate e più adattabili.
Un salto di poli, in conclusione, apre la possibilità di estinzioni di massa e l’inizio di un processo di evoluzione molto intenso, con la diffusione a livello globale di nuove specie.
È importante notare che la Terra non potrebbe in alcun modo mantenere ininterrottamente il proprio asse di rotazione verticale rispetto all’eclittica, a causa della presenza della luna. Il nostro satellite ha un’orbita inclinata di 5 gradi rispetto all’eclittica, pertanto eserciterebbe una coppia perturbatrice sulla Terra che la costringerebbe a precedere: il “tilt” aumenterebbe fino ad un massimo di 12/15 gradi, per poi diminuire nuovamente, con periodo di circa 15/20 mila anni.
Con l’aumentare del tilt crescerebbero le temperature estive e quindi la quantità di ghiaccio sciolto durante la bella stagione. I ghiacci polari e quelli montani, quindi, si ritirerebbero, per avanzare nuovamente con il diminuire del tilt. Si avrebbero cioè periodiche avanzate e ritirate delle calotte glaciali in tutto il mondo, proprio come si è verificato durante l’ultima glaciazione pleistocenica. A queste macroscopiche variazioni periodiche vanno aggiunti gli effetti di altri fattori che hanno una qualche influenza sul clima, come i cicli astronomici di Milankovitch, le variazioni di gas- serra e così via.
Dal momento che si parla di gas-serra, è interessante notare che dai carotaggi nei ghiacci dell’Antartide e della Groenlandia risulta in modo netto che la loro concentrazione nell’atmosfera varia sempre “dopo” i cambiamenti climatici, mai prima. Questo significa che per ogni condizione climatica della Terra esiste una ben determinata concentrazione di gas serra che si mantiene stabilmente.
Al giorno d’oggi l’equilibrio è rotto dalla massiccia produzione di CO2 a causa delle attività umane. Questo avrà certamente effetti sul clima terrestre, che però non dovrebbero essere permanenti. Quando gli uomini smetteranno di introdurre gas-serra nell’atmosfera, la loro concentrazione dovrebbe tornare, prima o poi, in condizioni di equilibrio.
Probabilità che un impatto dia luogo ad un salto di poli
Perché l’impatto da parte di un corpo celeste dia luogo ad un salto dei poli, è necessario che siano verificate le due seguenti condizioni:
a) che la coppia d’impatto sia sufficiente a eguagliare la coppia di reazione massima della Terra nella direzione dell’urto, anche per un solo istante. Ciò significa che non solo il corpo deve avere massa e velocità adeguate, ma che anche il braccio della coppia deve essere sufficientemente ampio .
b) La coppia di attrazione lunisolare sui rigonfiamenti terrestri deve avere lo stesso segno di quella sviluppata dall’impatto.
Questa seconda condizione ha chiaramente una probabilità di essere verificata del 50%. Quindi, in ogni caso la probabilità che un impatto dia luogo ad un salto di polo è inferiore a questo valore, qualunque sia la grandezza dell’oggetto. Relativamente indipendente dalla massa dell’oggetto è anche la probabilità che esso possa sviluppare una coppia di valore adeguato.
Determinante a tal fine, infatti, è il valore del “braccio” della coppia. Se l’urto è diretto esattamente verso il centro della Terra, non si ha nessuna coppia, qualunque sia la massa e velocità dell’oggetto. Viceversa, se l’impatto è molto angolato, quasi tangente alla superficie terrestre, anche un oggetto di modeste dimensioni può sviluppare una coppia rilevante. Significativa ai fini del valore del picco di accelerazione, e quindi della coppia sviluppata, dovrebbe essere anche la compattezza o meno dell’oggetto e la natura del terreno nel punto dell’impatto.
I calcoli effettuati nell’appendice matematica mostrano che asteroidi relativamente piccoli, con un diametro dell’ordine di qualche centinaio di metri, sarebbero in grado di innescare un salto di poli.
Gli oggetti Apollo
La probabilità che la Terra venga colpita da un asteroide di queste dimensioni è piuttosto alta. Responsabile è una particolare categoria di asteroidi chiamati dagli astronomi “oggetti Apollo”, o più sovente NEO (Near Earth Objects), la cui caratteristica è che la loro orbita interseca quella terrestre.
A tutto il 2012 il numero totale di asteroidi di questa classe con diametro superiore a 100 metri scoperti dagli astronomi ammonta a 1480, ma il numero totale di quelli effettivamente esistenti è stimato intorno ai 4700. Di questi almeno un migliaio avrebbero un diametro superiore al chilometro.
|
Le orbite degli asteroidi scoperti fino al 2013, che intersecano l'orbita della Terra e che hanno quindi una qualche probabilità di colpirla. (fonte:Focus) |
|
La probabilità che un NEO colpisca la Terra è stimata in 5.10-9 per anno per ogni singolo oggetto. Pertanto si calcola una probabilità di almeno 4 collisioni per ogni milione di anni con oggetti di almeno 1 chilometro di diametro. Mano a mano che le dimensioni diminuiscono, questa probabilità aumenta esponenzialmente, fino a divenire dell’ordine di un impatto ogni pochi secoli per oggetti superiori a 100 metri.
La probabilità calcolata concorda, in quanto ordine di grandezza, con la statistica degli impatti subiti dalla Terra negli ultimi 600 milioni di anni (G.W. Wetherill, “Gli Oggetti Apollo”, Scientific American ,Maggio 79 - Tom Gehrels, “Collision with comets and asteroids”, Scientific American, march 96) . Se la Terra fosse priva di oceani e atmosfera presenterebbe una superficie butterata di crateri come quella della luna e di Mercurio.
|
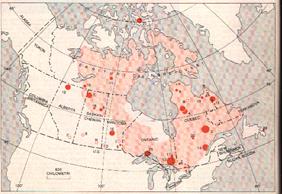
Sul nostro pianeta, invece, i processi di erosione e sedimentazione cancellano rapidamente le tracce degli impatti meteoritici. Ma in zone particolari, come ad esempio lo scudo canadese, che sono state recentemente raschiate dai ghiacci, le tracce degli antichi impatti sono state rimesse a nudo ed è possibile quindi farne una conta precisa. Sulle base di esse G. W. Wetherill ha valutato che il pianeta, negli ultimi 600 milioni di anni, sia stato colpito da almeno 1500 oggetti aventi un diametro superiore ad un chilometro; in buon accordo, quindi con le stime calcolate. |
|
Un calcolo molto prudenziale (vedi la seguente appendice matematica) dimostra che un asteroide litico del diametro di 1 km è ampiamente sufficiente ad innescare un salto di poli. Dai calcoli risulta che oggetti grandi la metà o anche meno siano in grado di sviluppare coppie perturbatrici che superano la soglia richiesta.
La probabilità che la Terra venga colpita da corpi di questa grandezza è piuttosto alta, probabilmente dell’ordine delle decine ogni milione di anni. Pertanto i salti di poli dovrebbero essere eventi piuttosto frequenti e dovrebbero giocare un ruolo fondamentale nella storia geologica della Terra.
La maggior parte degli impatti passa inosservata, ma basta dare un’occhiata a quelli che si sono stati registrati nei primi 13 anni del terzo millennio (fonte: rivista Focus) per rendersi conto di quanto siano frequenti.
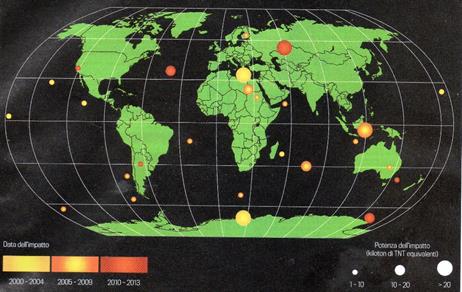
Una quindicina hanno sviluppato una potenza compresa fra 1 e 10 kilotoni, almeno 4 una potenza fra 10 e 20 kilotoni ed altrettanti una potenza superiore. Erano tutti oggetti molto piccoli, inferiori alla decina di metri, o poco più, e la maggior parte sono esplosi in mare o nell’atmosfera, senza provocare danni.
Bibliografia
- Charles Hapgood, “The
Path of the Pole”, Chilton Book Co, Philadefphia, 1970
- R. F. Deimel,
“Mechanics of the gyroscope. The dinamics of rotation”, Dover Edition, 1950
- G.W. Wetherill, “ The
Apollo objects”’Scientific American, May 79
- Tom Geherels,
“Collision with Comets and Asteroids”’ Scientific American, March 96
- E. Spedicato, “Apollo objects, Atlantis and
the deluge: a catastrophical scenario for the end of the last glaciation”
- A. Allam and P.B. Wignall, Mass Extinctions and their aftermath, Oxford, 2000
vedi successivo:
Atlantide, la madre di tutte le civiltà antiche
Torna a:
Condizioni climatiche della Terra nel Pleistocene
Torna a:
pagina iniziale
APPENDICE MATEMATICA
Componenti rotazionali di un giroscopio libero perturbato
Le componenti rotazionali in un giroscopio libero perturbato sono legate fra loro dalla seguente relazione, dovuta al Laplace, la quale esprime il principio della conservazione dell’energia:
1) Jo W2 = Jo w2 + Jp wp2 = Ji wi 2
dove:
W = velocità di rotazione del giroscopio non perturbato
w = velocità di rotazione del giroscopio intorno al suo asse principale
wp = velocità di
precessione
wi =
velocità di rotazione istantanea del giroscopio
Jo = momento d’inerzia principale del
giroscopio
Jp = momento d’inerzia rispetto
all’asse di precessione
Ji = momento d’inerzia rispetto
all’asse di rotazione istantanea
Il valore della coppia perturbatrice sviluppata da una forza generica Fp, formante un angolo b con l’asse di figura del giroscopio, è dato evidentemente dalla:
2) Cp = R Fp senb
dove R è il braccio della forza, ossia la distanza del suo punto di applicazione dal centro del giroscopio.
Il movimento di precessione wp del giroscopio avviene sempre intorno ad un asse equatoriale, che però è diverso istante per istante in modo tale che l’asse di figura viene a muoversi su una superficie conica, con vertice al centro e apertura 2 b. Esso viene quindi a ruotare con velocità angolare wpa intorno ad un asse parallelo alla forza stessa, che chiameremo asse di precessione apparente, per distinguerlo da wp (vedi fig. 1).
Il valore della wpa è dato dalla formula:
3) 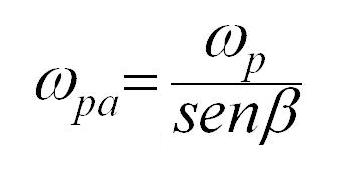
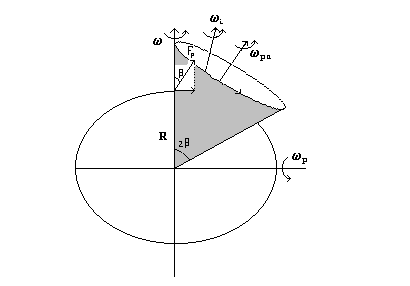
fig.1
Le relazioni 1), 2) e 3) consentono di studiare esaurientemente il comportamento di un giroscopio libero perturbato, con un metodo essenzialmente grafico.
Dato un giroscopio, disegniamo, sulla base della sua ellisse di inerzia, un’altra ellisse i cui semiassi siano rispettivamente:
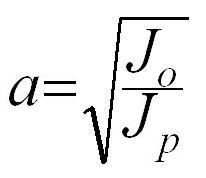
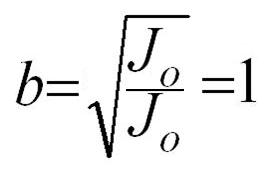
Ciascun raggio dell’ellisse r(q) , con q = 0 ¸ 2p, avrà ovviamente il valore:
![]()
dove J q è il momento d’inerzia di un asse formante un angolo q con quello di figura.
Posto W2 = 1 , per la 1) ciascun raggio r(q) è proporzionale alla velocità angolare che il giroscopio deve avere intorno all’asse q per mantenere invariata l’energia iniziale (vedi fig.2)
Le estremità delle frecce rappresentanti W ed wi , quindi, cadono sempre sull’ellisse, mentre tutte le altre componenti rotazionali si trovano sempre all’interno di essa. Questa ellisse consente di analizzare esaurientemente il comportamento delle varie componenti rotazionali del giroscopio, legate come sono dalla relazione 1).
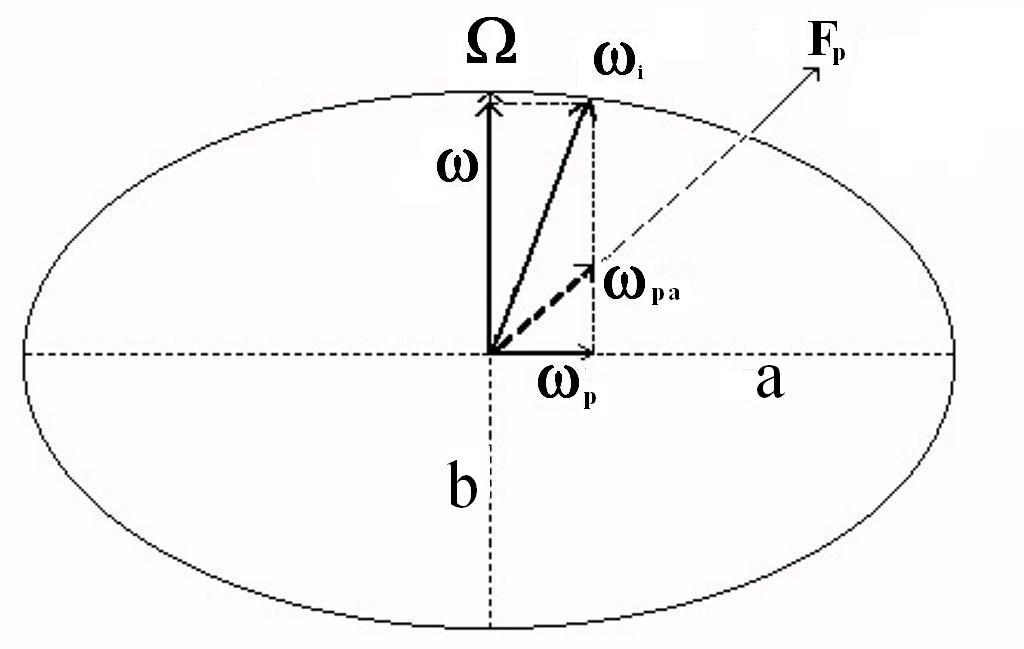
fig. 2
Il significato di queste
componenti è facilmente intuibile. Un giroscopio soggetto ad una coppia di
ribaltamento reagisce sviluppando una coppia esattamente uguale e contraria.
Questo viene ottenuto ruotando istante per istante intorno ad un asse, wi , diverso da
quello di figura e tanto più sbilanciato quanto più grande è la coppia
perturbatrice. La wi è la risultante
del movimento di rotazione attorno all’asse di figura e della rotazione,
wp, attorno ad un
asse equatoriale. In ogni istante si ha ovviamente:
wi2 = w2 + wp2.
Quando un giroscopio è soggetto ad una coppia perturbatrice Cp, di valore crescente, wp cresce, per cui la wi si sposta in direzione della wpa.
Quando la Fp raggiunge un valore Fpa uguale a quello sviluppato dal giroscopio ruotante intorno all’asse di wpa (vedi calcoli più avanti),avremo evidentemente:
wi = wpa.
In questo momento l’asse di rotazione istantanea viene a coincidere con l’asse di precessione apparente. E’ questa una condizione particolarissima in cui il sistema costituito dal giroscopio e dalla coppia perturbatrice si comporta come un giroscopio non perturbato, con un’unica componente rotazionale, W’, fissa rispetto allo spazio ed al corpo giroscopico stesso, il cui asse diventa asse di rotazione principale del sistema.
Se a questo punto la forza Fp torna a diminuire, il sistema di comporta come un giroscopio cui venga applicata una coppia di valore:
C’p = Cpa - Cp
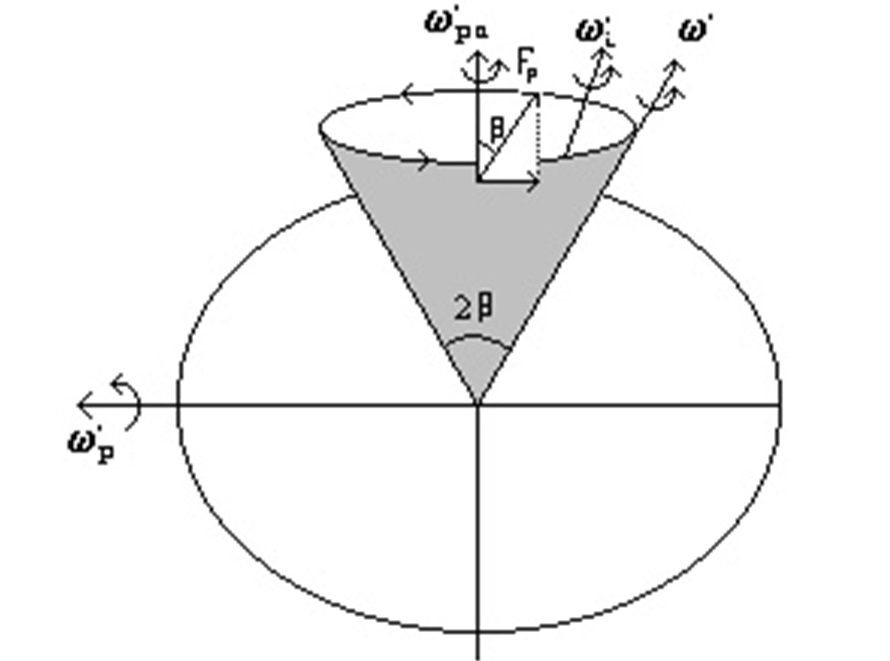
fig. 3
Il nuovo asse di rotazione comincia pertanto a precedere intorno all’asse di figura; la wi’, di conseguenza ripercorre il cammino inverso, portandosi in direzione di quest’ultimo. Il valore e la direzione delle varie componenti rotazionali del giroscopio in questo caso sono rappresentati in fig.3 e 4.
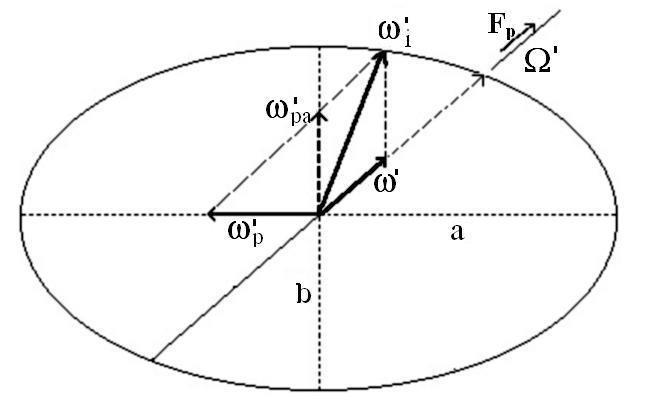
fig. 4
Per il principio di conservazione dell’energia, si avrà evidentemente:
Jpa W’2 = Jo w’2 + J’pwp’2 = Ji wi’2 = Jo W2
A parità di forza perturbatrice Fp, la velocità di rotazione istantanea è esattamente la stessa sia nel tragitto di “andata” che in quello di “ritorno”. Si ha cioè sempre wi’ = wi . Variano invece in maniera sostanziale le altre componenti rotazionali. In particolare w’p ha direzione opposta a wp . Questo si giustifica con il fatto che mentre nel tragitto di “andata” è l’asse di figura che ruota intorno all’asse di wpa , in quello di “ritorno” avviene il contrario, e cioè l’asse di wpa, che ora è fisso rispetto al corpo del giroscopio, viene a ruotare intorno a quello di figura.
Essenziale è il fatto che lungo l’asse di wpa si ha una componente rotazionale fissa rispetto al corpo del giroscopio. Ciò significa che il giroscopio conserva “memoria” della posizione del nuovo asse di rotazione. La componente rotazionale, e con essa la “memoria”, vengono cancellate soltanto quando la Fp si annulla totalmente. Se la Fp non dovesse annullarsi, il giroscopio conserverebbe indefinitamente due componenti rotazionali, entrambi intorno ad assi fissi rispetto a se stesso.
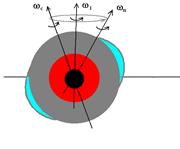
Comportamento di un giroscopio semifluido come la Terra
Il comportamento della Terra in presenza di una coppia perturbatrice è assimilabile a quello di un giroscopio, con una importante differenza, dovuta al fatto che il pianeta non è un solido omogeneo e indeformabile, ma è costituito da parti interne ed esterne liquide e da un guscio solido intermedio, dotato di alta plasticità e facilmente deformabile sotto l’effetto delle forze centrifughe. Ogni componente rotazionale del pianeta esercita sulle sue parti una forza centrifuga, in conseguenza della quale si hanno deformazioni e/o movimenti di massa, che a loro volta influiscono sulle componenti rotazionali e tendono costantemente ad annullare ogni eventuale coppia di reazione.
Se ad esempio costringiamo un giroscopio indeformabile a ruotare intorno ad un asse diverso da quello di figura, esso sviluppa una coppia di reazione che rimane costante nel tempo.
Anche la Terra, costretta a ruotare intorno ad un asse diverso da quello di figura, svilupperebbe inizialmente una coppia di reazione. La stessa forza centrifuga responsabile di questa coppia, tuttavia, agirebbe sulle masse plastiche e liquide, provocando deformazioni e/o spostamenti, tendenti a ricostituire l’ellissoide intorno al nuovo asse di rotazione. Di conseguenza la coppia di reazione diminuirebbe, fino ad annullarsi completamente dopo un certo tempo.
Noi non conosciamo forze in grado di costringere la Terra a ruotare intorno ad un asse diverso da quello di figura per un tempo sufficientemente lungo a completare un tale processo. Sappiamo, però, che il pianeta viene periodicamente colpito da grandi bolidi ad alta velocità, i quali sviluppano una coppia di ribaltamento di durata molto breve, ma che può avere un valore di picco assai elevato, dello stesso ordine di grandezza della coppia di reazione massima sviluppabile dalla Terra (vedi al paragrafo successivo i relativi calcoli).
Vediamo, con l’ausilio dei grafici di fig.2 e 4 cosa succede in questo caso.
Non appena la coppia sviluppata dall’impatto comincia a crescere, la wi si porta in direzione della wpa , parallela alla direzione dell’urto, fino a coincidere con essa se l’impatto sviluppa una coppia impulsiva di intensità sufficiente. In quell’istante l’asse di wpa diventa asse permanente. Non appena la coppia impulsiva diminuisce, l’asse wi torna velocemente in corrispondenza di quello di figura iniziale, ma con modalità radicalmente diverse da quelle del tragitto di “andata”, come si vede da fig. 4 Non appena l’impulso cessa, un attimo dopo, la Terra dovrebbe tornare nuovamente a ruotare intorno al suo asse naturale e tutto dovrebbe finire lì, ma non è detto.
Perché la “memoria” del nuovo asse di rotazione venga cancellata ed il giroscopio torni a ruotare intorno all’asse di figura, è necessario che la coppia perturbatrice si annulli “completamente”. Purtroppo, ci sono buone probabilità che questo non avvenga. Sappiamo che la Terra è soggetta in permanenza ad una coppia perturbatrice dovuta all’attrazione gravitazionale esercitata dal sole e dalla luna sui rigonfiamenti equatoriali. Questa coppia è di un ordine di grandezza dieci milioni di volte più piccolo di quella sviluppata dall’urto; ma il suo ruolo è fondamentale.
Se al momento dell’impatto essa ha segno contrario rispetto a quello sviluppato nell’urto, appena l’impulso si esaurisce, la Terra recupera istantaneamente il primitivo asse di rotazione e tutto finisce lì. Gli unici effetti sarebbero quelli distruttivi immediati prodotti dall’impatto.
Se invece essa ha inizialmente la stessa direzione della coppia impulsiva prodotta dal bolide, si somma a quest’ultima e contribuisce, nel suo piccolo, allo spostamento subitaneo della posizione dei poli. Pochi istanti dopo, la coppia impulsiva si annulla, ma quella lunisolare rimane e, per quanto piccola, è pur sempre maggiore di zero e quindi sufficiente ad impedire che la “memoria” dell’asse intorno a cui la Terra ha ruotato per un breve istante venga cancellata.
In questo caso la Terra viene a comportarsi in realtà come un giroscopio con asse di figura coincidente con quello assunto nell’istante dell’impatto, soggetto ad una coppia perturbatrice costante, di entità praticamente uguale e segno contrario a quella impulsiva sviluppata dal bolide. Vediamo in figura 5 la situazione che si viene a determinare in questo caso.
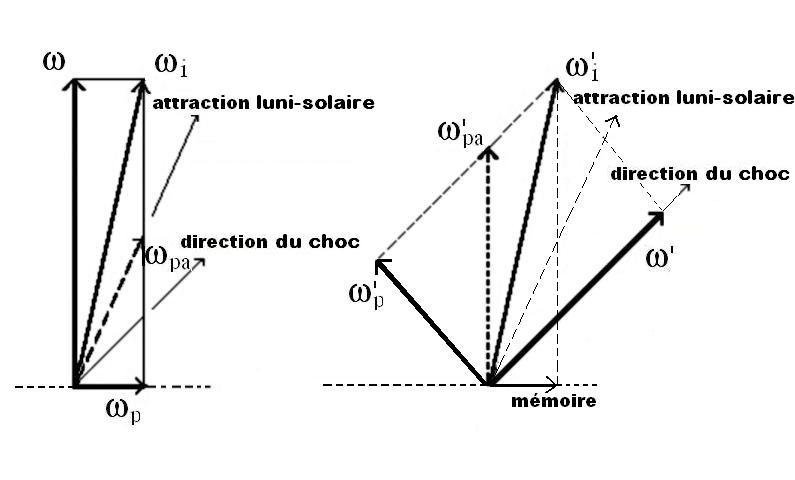
a b
fig.5
I grafici 5.a e 5.b rappresentano la situazione delle componenti rotazionali della Terra immediatamente prima (a) e dopo (b) l’impatto, nel caso in cui la coppia lunisolare abbia lo stesso segno di quella sviluppata dall’urto. (Nella figura le componenti rotazionali di precessione sono molto esagerate, ai fini esplicativi; in realtà sono dell’ordine del milione di volte più piccole della rotazione principale. Il ragionamento, tuttavia, non cambia).
La situazione in apparenza non è cambiata, perché wi è esattamente uguale ad w’i, ed anche w’ è dello stesso ordine di grandezza della velocità di precessione iniziale wpa, milioni di volte più piccola della rotazione principale .
C’è però una differenza fondamentale: a questo punto la w’ è l’unica componente rotazionale “fissa” rispetto al corpo della Terra. L’asse di w’ , quindi, è asse di rotazione permanente e per quanto piccola sia la rotazione intorno ad esso (un milione di volte più piccola della rotazione principale), esso esercita pur sempre una forza centrifuga, debolissima, che tende a formare un rigonfiamento equatoriale rispetto al proprio asse (che sarebbe dell’ordine della decina di metri).
Se la Terra fosse un giroscopio rigido indeformabile, questa situazione permarrebbe immutata indefinitamente. Il pianeta, però, è coperto da un sottile strato di acqua, molto pronta a reagire ad ogni cambiamento di moto.
Si comincia quindi con l’avere un leggero spostamento di liquidi verso la nuova linea equatoriale. Mano a mano che ciò avviene, la w’ torna ad aumentare, quindi cresce la forza tendente a far spostare i liquidi verso il nuovo equatore, e così via, in un processo che parte molto lentamente, ma va via via accelerandosi fino a che la forza centrifuga non diviene sufficiente far deformare il guscio plastico. Dopo un certo tempo, quindi, l’ellissoide si ricostituisce intorno al nuovo asse di rotazione, e la Terra torna nuovamente in condizioni di stabilità, ma con asse di rotazione e poli spostati.
Valore della coppia di reazione della Terra
Il valore della coppia di reazione di un giroscopio, quando ruota intorno ad un asse diverso da quello di figura, può ricavarsi (vedi fig. 6), considerando la coppia elementare sviluppata dall’elemento di massa dm, che gira intorno all’asse di rotazione istantanea wi:
Ci = Fi b
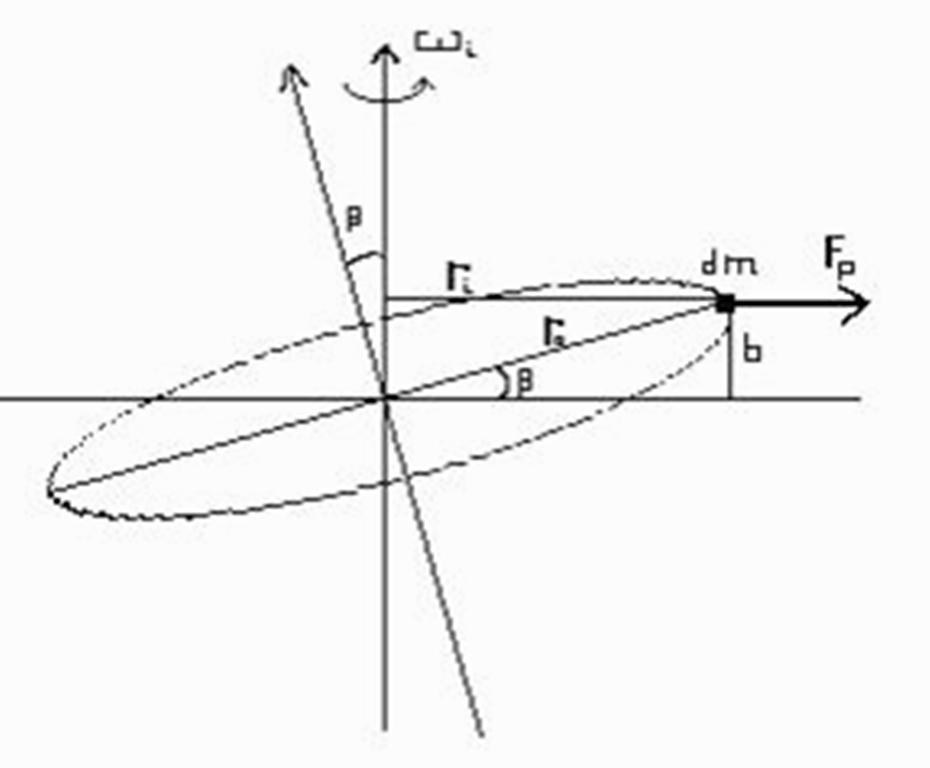
fig. 6
dove:
Fi = dm wi2 r i = dm wi2 ro cos b è la forza centrifuga;
b = ro senb è il braccio della coppia.
Avremo perciò:
Ci = dm ro2 wi2 senb cosb = dJo wi2 senb cosb = ½ dJo wi2 sen2b
dove dJo = dm ro2 è il momento d’inerzia della massa dm rispetto all’asse principale.
Per un giroscopio costituito da un ellissoide di rotazione avremo pertanto (vedi fig. 7):
4) C = (Jo - Jp) wi2 senbcosb = ½ Jr wi2 sen2b
dove Jr = (Jo - Jp) è il momento d’inerzia del solo rigonfiamento equatoriale.
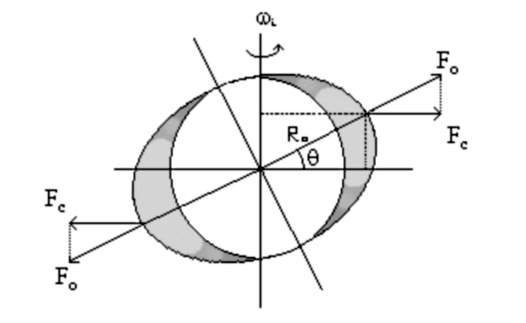
Dalla relazione 4) si vede che un giroscopio è in grado di sviluppare una coppia di reazione soltanto quando Jo ¹ Jp. Se fosse una sfera perfetta, infatti, esso ruoterebbe indifferentemente intorno ad un qualsiasi asse e non si avrebbe alcuna componente stabilizzante. In una sfera omogenea, infatti, tutte le forze centrifughe si bilanciano reciprocamente e non si ha alcuna coppia di reazione, qualunque sia l’asse di rotazione. Soltanto i ‘rigonfiamenti” sviluppano una coppia di reazione, quando ruotano intorno ad un asse diverso da quello di figura
Valore della coppia stabilizzante sviluppata dai rigonfiamenti terrestri
Dalla 4) si vede che la coppia di reazione massima sviluppabile da un giroscopio è:
Cm = ½ Jr wi2
Il valore di wi è sensibilmente uguale a quello della rotazione normale, per cui possiamo porre:
wi2 » (2p / 8,64)2 1010 = 5,28 . 109
Il calcolo della Jr può essere fatto in modo indiretto, utilizzando i calcoli sviluppati da Gallen e da Deininger per conto dello stesso Hapgood (vedi riquadro a parte), la forza centrifuga sviluppata dai rigonfiamenti equatoriali per effetto della rotazione terrestre è pari a:
Fo = 4,1192. 1019 kg.
Per un calcolo approssimativo possiamo porre:
Jr @ Mr Ro2
Fo @ Mr wi2 Ro2 = Jr wi2 / Ro
dove Mr è la massa dei rigonfiamenti ed Ro il raggio della Terra.
Si ha quindi:
Jr = Fo Ro / wi2 @ 5 1034 kgmt2
Ed infine, grazie all’equazione 4), avremo:
4’) C = ½ Jr wi2 sen2b = 1,38 sen2b kgmt.
Per b = 45o avremo:
C @ 1,38 1026 kgmt
che è la massima coppia di reazione sviluppabile dalla Terra.
Calcolo della massa che un asteroide deve possedere
per provocare un salto di poli
Per la relazione 4) un asteroide che colpisca la Terra, per spostare l’asse di rotazione di un certo angolo, ad esempio di 20° (per un solo istante si intende), deve poter sviluppare una coppia impulsiva di valore:
C20° = 8,87 . 10 25 Kgmt.
E’ pertanto immediato calcolare le caratteristiche dimensionali e cinematiche che tale corpo deve possedere.
La forza impulsiva Fi sviluppata nell’impatto con la Terra è data dalla formula classica:
Fi = Ma a
dove
a = dv/dt è l’accelerazione che il corpo subisce nell’impatto
Ma è la massa dell’asteroide
Per il calcolo dell’accelerazione, a, possiamo assumere che l’asteroide al momento dell’impatto abbia una velocità, v, compresa fra 25 e 75 km/sec., cioè la media di quella constatata per gli oggetti Apollo. Poniamo pertanto:
v = 5 . 10 4 mt/sec.
Per il calcolo di dt dobbiamo affidarci ad una stima. In via del tutto prudenziale, basandoci sulla profondità dei crateri conosciuti, possiamo assumere che la profondità del cratere provocato dall’impatto sia di ½ km; ciò significa che la velocità del corpo passa da 5.104 mt/sec a 0, nello spazio di ½ chilometro. Possiamo valutare l’intervallo di tempo in cui ciò avviene nell’ordine del centesimo di secondo, cioè:
dt = 0,01 sec.
L’accelerazione media subita dal corpo sarà pertanto:
am = dv/dt = 5.104 / 0,01 = 5. 106 m/sec2
Il picco di accelerazione è certamente molto superiore; per un calcolo prudenziale possiamo assumere che sia il doppio del valore medio. Si avrà pertanto:
a = 5.10 4 / 0.005 = 10 7 mt/sec2
E pertanto si avrà:
Fi = Ma . 10 7 kg
La coppia sviluppata da questa forza sarà evidentemente :
Ci = Fi . Ri
dove: Ri è il braccio della forza.
Il valore di Ri può essere compreso fra 0 e Ro@6,4 106 mt., e cioè il valore del raggio terrestre. Per ragioni statistiche possiamo porre:
Ri = ½ Ro = 3,2 106 mt
Il valore della massa dell’asteroide sarà pertanto:
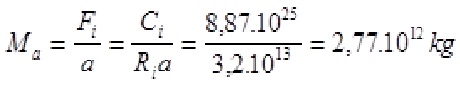
Supposto che il corpo abbia una densità di 3 Kg/dm3, si ha un volume di:
Va = 0,92 km3
Un asteroide litico, quindi, del diametro dell’ordine del chilometro. Questo calcolo, tuttavia, è prudenziale, per cui possiamo realisticamente ritenere che un oggetto avente un diametro dell’ordine del mezzo chilometro sia ampiamente sufficiente a sviluppare una coppia del valore richiesto per un salto di poli di grande ampiezza.
Calcoli eseguiti dal Dot.. F.L. Gallen, direttore del
“Department of
Commerce U.S. Coast and Geodetic Survey”,Washington
Siano le equazioni della sfera e dell’ellissoide di rotazione rispettivamente:
1) x2 + y2 + z2 = b2
2)
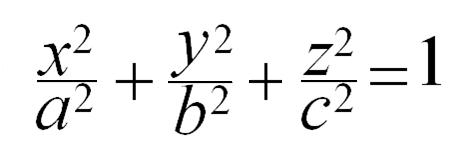
dove l’asse y è l’asse di rivoluzione. Sia dM la massa dell’anello generato dalla rotazione del rettangolo dxdy intorno all’asse y. Avremo:
3) dM = 2pdx dxdy
dove d è la densità. Per ogni particella dell’anello l’accelerazione centrifuga è la stessa, ed è uguale ad w2 x, dove w è la velocità angolare in radianti al secondo.
La forza centrifuga dF esercitata dall’anello è data quindi dalla:
4) dF = w2x dM = 2pdw2x2 dxdy
Integrando l’equazione 4) rispetto ad x ed y avremo:
5)
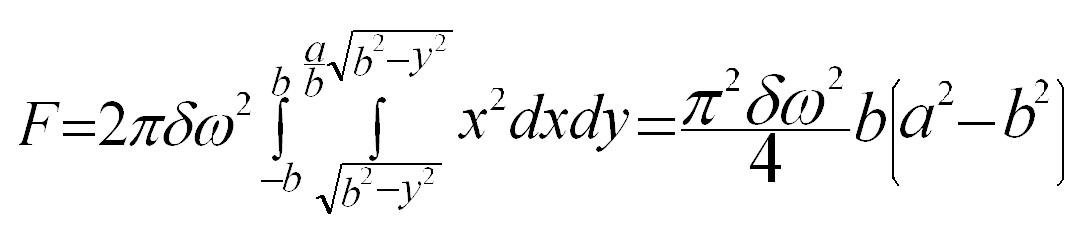
Nell’espressione 5) F è espresso in dine, quando d è in grammi per centimetro cubo e a e b in centimetri. La quantità w può essere sostituita con 2pn, dove n è il numero dei giri per secondo. La Terra esegue un giro completo mediamente in 86.164,09 secondi solari, per cui n = 7,28 10-5.
Calcolo della forza centrifuga effettuato dal Dott. Deininger (Smith College) sulla base della formula di Gallen
Calcolo della forza centrifuga prodotta dalla forza rotazione dei rigonfiamenti equatoriali:
A. Dati essenziali:
La formula 5) è applicata considerando lo spessore del rigonfiamento di 13,3443 miglia all’equatore, in diminuzione graduale fino ad annullarsi ai poli.
Calcolo:
1)
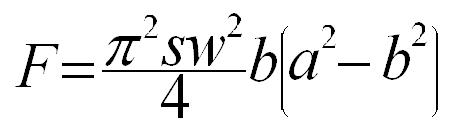
dove:
s = densità in gr/cm3
a = raggio terrestre all’equatore in cm
b = raggio terrestre ai poli in cm
w = 2 - n r = rps
2) F = p4sn2. b(a3 - b3)
dove:
s = 2,7 gm/cm3
n = 1/86.164
b = 6,402 . 108 cm
a = 6,4165 . 108 cm
3) F = 4,0368 . 1025 dine = 4,1192. 1019 kg.
- Torna a: "home"
- Torna a: "Civiltà misteriose"
- Acquista un libro